江苏省苏锡常镇四市高三教学情况调研一理科数学试卷
在一次满分为160分的数学考试中,某班40名学生的考试成绩分布如下:
| 成绩 |
80分以下 |
[80,100) |
[100,120) |
[120,140) |
[140,160] |
| 人数 |
8 |
8 |
12 |
10 |
2 |
在该班随机抽取一名学生,则该生在这次考试中成绩在120分以上的概率为 .
如图,四棱锥P-ABCD中, ⊥底面
⊥底面 ,底面
,底面 是矩形,
是矩形, ,
, ,
, ,
,
点E为棱CD上一点,则三棱锥E-PAB的体积为 .
在平面直角坐标系xOy中,已知圆C: ,点A是
,点A是 轴上的一个动点,AP,
轴上的一个动点,AP,
AQ分别切圆C于P,Q两点,则线段PQ长的取值范围为 .
如图,四边形 为矩形,四边形
为矩形,四边形 为菱形,且平面
为菱形,且平面 ⊥平面
⊥平面 ,D,E分别为边
,D,E分别为边 ,
, 的中点.
的中点.
(1)求证: ⊥平面
⊥平面 ;
;
(2)求证:DE∥平面 .
.
如图,有一段河流,河的一侧是以O为圆心,半径为 米的扇形区域OCD,河的另一侧是一段笔直的河岸l,岸边有一烟囱AB(不计B离河岸的距离),且OB的连线恰好与河岸l垂直,设OB与圆弧
米的扇形区域OCD,河的另一侧是一段笔直的河岸l,岸边有一烟囱AB(不计B离河岸的距离),且OB的连线恰好与河岸l垂直,设OB与圆弧 的交点为E.经测量,扇形区域和河岸处于同一水平面,在点C,点O和点E处测得烟囱AB的仰角分别为
的交点为E.经测量,扇形区域和河岸处于同一水平面,在点C,点O和点E处测得烟囱AB的仰角分别为 ,
, 和
和 .
.
(1)求烟囱AB的高度;
(2)如果要在CE间修一条直路,求CE的长.
在平面直角坐标系xOy中,已知椭圆C:
 的离心率为
的离心率为 ,且过点
,且过点 ,过椭圆的左顶点A作直线
,过椭圆的左顶点A作直线 轴,点M为直线
轴,点M为直线 上的动点,点B为椭圆右顶点,直线BM交椭圆C于P.
上的动点,点B为椭圆右顶点,直线BM交椭圆C于P.
(1)求椭圆C的方程;
(2)求证: ;
;
(3)试问 是否为定值?若是定值,请求出该定值;若不是定值,请说明理由.
是否为定值?若是定值,请求出该定值;若不是定值,请说明理由.
已知函数 .
.
(1)当 时,求
时,求 的单调减区间;
的单调减区间;
(2)若方程 恰好有一个正根和一个负根,求实数
恰好有一个正根和一个负根,求实数 的最大值.
的最大值.
已知数列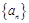 的前n项和为
的前n项和为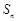 ,设数列
,设数列 满足
满足 .
.
(1)若数列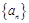 为等差数列,且
为等差数列,且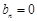 ,求数列
,求数列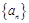 的通项公式;
的通项公式;
(2)若 ,
,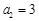 ,且数列
,且数列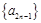 ,
,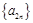 都是以2为公比的等比数列,求满足不等式
都是以2为公比的等比数列,求满足不等式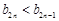 的所有正整数n的集合.
的所有正整数n的集合.
如图,AB为圆O的切线,A为切点,C为线段AB的中点,过C作圆O的割线CED(E在C,D之间),求证:∠CBE=∠BDE.
在极坐标系中,曲线C的极坐标方程为 ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为 (
( 为参数),求直线
为参数),求直线 被曲线
被曲线 所截得的弦长.
所截得的弦长.
如图,在四棱锥P-ABCD中, 底面ABCD,底面ABCD是边长为2的菱形,
底面ABCD,底面ABCD是边长为2的菱形, ,
, ,M为PC的中点.
,M为PC的中点.
(1)求异面直线PB与MD所成的角的大小;
(2)求平面PCD与平面PAD所成的二面角的正弦值.
 ,则
,则 .
. (i为虚数单位)为纯虚数,则实数
(i为虚数单位)为纯虚数,则实数 .
. 的离心率为 .
的离心率为 . 的定义域为 .
的定义域为 . 的值为 .
的值为 .
 的各项均为正数,若
的各项均为正数,若 ,
, ,则
,则 .
. 与曲线
与曲线 在
在 处的两条切线互相垂直,则实数
处的两条切线互相垂直,则实数 的值为 .
的值为 . 的最小正周期为
的最小正周期为 ,且满足
,且满足 ,则函数
,则函数 的单调增区间为 .
的单调增区间为 . ,
, ,且
,且 ,则
,则 .
.
 与曲线
与曲线 恰有四个不同的交点,则实数k的取值
恰有四个不同的交点,则实数k的取值 满足
满足 ,且
,且 ,则
,则 的最小值为 .
的最小值为 . ,
, ,
, .
. ⊥
⊥ ,求
,求 的值;
的值; 的值.
的值. 在矩阵M
在矩阵M 对应的变换作用下得到的曲线所围成图形的面积.
对应的变换作用下得到的曲线所围成图形的面积. 的最大值.
的最大值. 个不同的正整数
个不同的正整数 ,对任意
,对任意 ,都有
,都有 ,则称这
,则称这 ,
, 构造一组“好数”;
构造一组“好数”; ,均存在“
,均存在“ 粤公网安备 44130202000953号
粤公网安备 44130202000953号