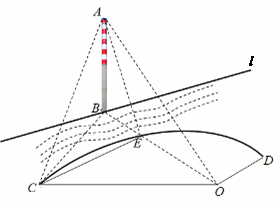
如图,有一段河流,河的一侧是以O为圆心,半径为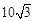 米的扇形区域OCD,河的另一侧是一段笔直的河岸l,岸边有一烟囱AB(不计B离河岸的距离),且OB的连线恰好与河岸l垂直,设OB与圆弧
米的扇形区域OCD,河的另一侧是一段笔直的河岸l,岸边有一烟囱AB(不计B离河岸的距离),且OB的连线恰好与河岸l垂直,设OB与圆弧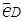 的交点为E.经测量,扇形区域和河岸处于同一水平面,在点C,点O和点E处测得烟囱AB的仰角分别为
的交点为E.经测量,扇形区域和河岸处于同一水平面,在点C,点O和点E处测得烟囱AB的仰角分别为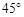 ,
,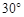 和
和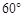 .
.
(1)求烟囱AB的高度;
(2)如果要在CE间修一条直路,求CE的长.
推荐套卷
如图,有一段河流,河的一侧是以O为圆心,半径为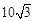 米的扇形区域OCD,河的另一侧是一段笔直的河岸l,岸边有一烟囱AB(不计B离河岸的距离),且OB的连线恰好与河岸l垂直,设OB与圆弧
米的扇形区域OCD,河的另一侧是一段笔直的河岸l,岸边有一烟囱AB(不计B离河岸的距离),且OB的连线恰好与河岸l垂直,设OB与圆弧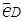 的交点为E.经测量,扇形区域和河岸处于同一水平面,在点C,点O和点E处测得烟囱AB的仰角分别为
的交点为E.经测量,扇形区域和河岸处于同一水平面,在点C,点O和点E处测得烟囱AB的仰角分别为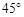 ,
,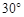 和
和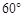 .
.
(1)求烟囱AB的高度;
(2)如果要在CE间修一条直路,求CE的长.