(本小题满分12分)设二次函数 ,关于
,关于 的不等式
的不等式
的解集有且只有一个元素.
(1)设数列 的前
的前 项和
项和 ,求数列
,求数列 的通项公式;
的通项公式;
(2)记 ,求数列
,求数列 中是否存在不同的三项能组成等比数列?请说明理由.
中是否存在不同的三项能组成等比数列?请说明理由.
已知函数 的图像与
的图像与 轴正半轴的交点为
轴正半轴的交点为 ,
, =1,2,3,….
=1,2,3,….
求数列 的通项公式;
的通项公式;
令 为正整数), 问是否存在非零整数
为正整数), 问是否存在非零整数 , 使得对任意正整数
, 使得对任意正整数 ,都有
,都有 ? 若存在, 求出
? 若存在, 求出 的值 , 若不存在 , 请说明理由.
的值 , 若不存在 , 请说明理由.
(本小题满分12分)如图,在四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD为梯形,BC∥AD,AB⊥AD,PA=AB=BC=1,AD=2.
(1)求三棱锥P—ACD的外接球的表面积;
(2)若M为PB的中点,问在AD上是否存在一点E,使AM∥平面PCE?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(本小题满分12分)设数列{an}的前n项和为Sn,对任意的正整数n,都有an=4Sn+1成立.
(1)求数列{an}的通项公式;
(2)设bn=log3|an|,数列{ }的前n项和为Tn, 求证:Tn<
}的前n项和为Tn, 求证:Tn< .
.
已知动点 到点
到点 的距离等于点
的距离等于点 到直线
到直线 的距离,点
的距离,点 的轨迹为
的轨迹为 .
.
(Ⅰ)求轨迹 的方程;
的方程;
(Ⅱ)设 为直线
为直线 上的点,过点
上的点,过点 作曲线
作曲线 的两条切线
的两条切线 ,
, ,
,
(ⅰ)当点 时,求直线
时,求直线 的方程;
的方程;
(ⅱ)当点 在直线
在直线 上移动时,求
上移动时,求 的最小值.
的最小值.
将单位正方体放置在水平桌面上(一面与桌面完全接触),沿其一条棱翻动一次后,使得正方体的另一面与桌面完全接触,称一次翻转.如图,正方体的顶点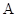 ,经任意翻转二次后,点
,经任意翻转二次后,点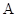 与其终结位置的直线距离不可能为( )
与其终结位置的直线距离不可能为( )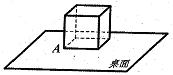
A. |
B.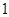 |
C.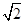 |
D.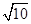 |
(本小题满分14分)
已知动点M到点 的距离等于M到点
的距离等于M到点 的距离的
的距离的 倍.
倍.
(1)求动点M的轨迹C的方程;
(2)若直线 与轨迹C没有交点,求
与轨迹C没有交点,求 的取值范围;
的取值范围;
(3)已知圆 与轨迹C相交于
与轨迹C相交于 两点,求
两点,求
定义在R上的函数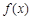 满足
满足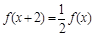 ,当
,当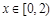 时,
时,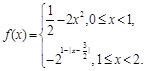 函数
函数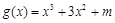 .若
.若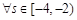 ,
,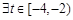 ,不等式
,不等式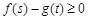 成立,则实数m的取值范围是( )
成立,则实数m的取值范围是( )
A.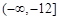 |
B. |
C.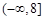 |
D.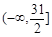 |
(本题满分18分)本题共3小题,第(1)小题6分,第(2)小题6分,第(3)小题6分.
已知函数 .
. 
(1)指出 的基本性质(结论不要求证明)并作出函数
的基本性质(结论不要求证明)并作出函数 的图像;
的图像;
(2)关于 的不等式
的不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)关于 的方程
的方程 (
( )恰有6个不同的实数解,求
)恰有6个不同的实数解,求 的取值范围.
的取值范围.
(本题满分16分)本题共3小题,第(1)小题4分,第(2)小题4分,第(3)小题8分.
已知数列 是公差不为
是公差不为 的等差数列,
的等差数列, 数列
数列 是等比数列,且
是等比数列,且 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,记点
,记点 .
.
(1)求数列 的通项公式;
的通项公式;
(2)证明:点 在同一直线
在同一直线 上,并求出直线
上,并求出直线 方程;
方程;
(3)若 对
对 恒成立,求
恒成立,求 的最小值.
的最小值.
(本小题满分14分)
已知抛物线 上一点
上一点 到其焦点F的距离为4;椭圆
到其焦点F的距离为4;椭圆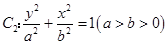 的离心率
的离心率 ,且过抛物线的焦点F.
,且过抛物线的焦点F.
(I)求抛物线 和椭圆
和椭圆 的标准方程;
的标准方程;
(II)过点F的直线 交抛物线
交抛物线 于A、B两不同点,交
于A、B两不同点,交 轴于点N,已知
轴于点N,已知 ,求证:
,求证: 为定值.
为定值.
(III)直线 交椭圆
交椭圆 于P,Q两不同点,P,Q在x轴的射影分别为
于P,Q两不同点,P,Q在x轴的射影分别为 ,
,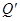 ,
, ,若点S满足:
,若点S满足: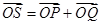 ,证明:点S在椭圆
,证明:点S在椭圆 上.
上.