上海市长宁区高三上学期教学质量检测理科数学试卷
已知函数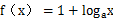 ,
,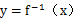 是函数y=f(x)的反函数,若
是函数y=f(x)的反函数,若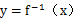 的图象过点(2,4),则a的值为______________.
的图象过点(2,4),则a的值为______________.
如图,圆锥的侧面展开图恰好是一个半圆,则该圆锥的母线与底面所成的角的大小是______________.
已知数列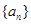 是以
是以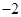 为公差的等差数列,
为公差的等差数列, 是其前
是其前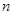 项和,若
项和,若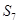 是数列
是数列 中的唯一最大项,则数列
中的唯一最大项,则数列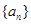 的首项
的首项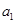 的取值范围是______________.
的取值范围是______________.
五位同学各自制作了一张贺卡,分别装入5个空白信封内,这五位同学每人随机地抽取一封,则恰好有两人抽取到的贺卡是其本人制作的概率是______________.
已知△ABC中,角A、B、C的对边分别为a、b、c,且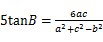 , 则
, 则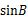 的值是______________.
的值是______________.
已知 的展开式中的常数项为
的展开式中的常数项为 ,
, 是以
是以 为周期的偶函数,且当
为周期的偶函数,且当 时,
时, ,若在区间
,若在区间 内,函数
内,函数 有4个零点,则实数
有4个零点,则实数 的取值范围是______________.
的取值范围是______________.
设z1、z2∈C,则“z +z
+z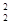 =0”是“z1=z2=0”的 ( )
=0”是“z1=z2=0”的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
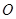 是△ABC所在平面内的一点,且满足
是△ABC所在平面内的一点,且满足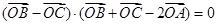 ,则△ABC的形状一定是( )
,则△ABC的形状一定是( )
| A.正三角形 | B.直角三角形 |
| C.等腰三角形 | D.斜三角形 |
下面有五个命题:
①函数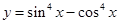 的最小正周期是
的最小正周期是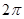 ;
;
②终边在y轴上的角的集合是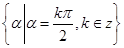 ;
;
③在同一坐标系中,函数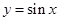 的图象和函数
的图象和函数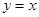 的图象有一个公共点;
的图象有一个公共点;
④把函数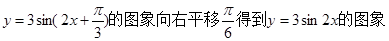 ;
;
⑤在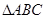 中,若
中,若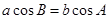 ,则
,则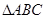 是等腰三角形
是等腰三角形 ;
;
其中真命题的序号是( )
| A.(1)(2)(3) | B.(2)(3)(4) |
| C.(3)(4)(5) | D.(1)(4)(5) |
如图:三棱锥P-ABC中,PA^底面ABC,若底面ABC是边长为2的正三角形,且PB与底面ABC所成的角为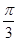 .若
.若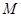 是
是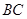 的中点,求:
的中点,求: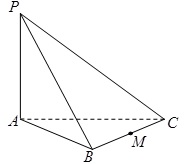
(1)三棱锥P-ABC的体积;
(2)异面直线PM与AC所成角的大小(结果用反三角函数值表示).
已知函数 的图像与
的图像与 轴正半轴的交点为
轴正半轴的交点为 ,
, =1,2,3,….
=1,2,3,….
求数列 的通项公式;
的通项公式;
令 为正整数), 问是否存在非零整数
为正整数), 问是否存在非零整数 , 使得对任意正整数
, 使得对任意正整数 ,都有
,都有 ? 若存在, 求出
? 若存在, 求出 的值 , 若不存在 , 请说明理由.
的值 , 若不存在 , 请说明理由.
已知函数 (
( 、
、 ),满足
),满足 ,且
,且 在
在 时恒成立.
时恒成立.
(1)求 、
、 的值;
的值;
(2)若 ,解不等式
,解不等式 ;
;
(3)是否存在实数 ,使函数
,使函数 在区间
在区间 上有最小值
上有最小值 ?若存在,请求出
?若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
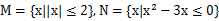 ,则M∩N
,则M∩N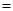 _______________.
_______________.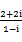 =______________.(
=______________.( 是虚数单位)
是虚数单位) 的前
的前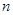 项和
项和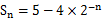 ,则其通项公式为
,则其通项公式为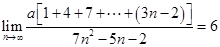 ,则
,则 ______________.
______________. 且
且 ,则复数
,则复数 对应点在第二象限的概率为______________.(用最简分数表示)
对应点在第二象限的概率为______________.(用最简分数表示)
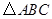 中,点
中,点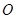 是
是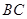 的中点,过点
的中点,过点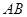 ,
,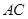 于不同的两点
于不同的两点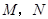 ,若
,若 ,
,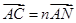 ,则
,则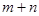 的值为 .
的值为 .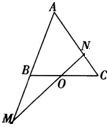
 的图象为( )
的图象为( )



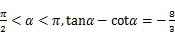
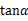 的值;
的值;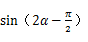 的值.
的值.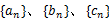 满足
满足
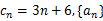 是公差为
是公差为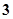 的等差数列.当
的等差数列.当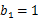 时,求
时,求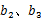 的值;
的值;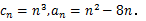 求正整数
求正整数 使得一切
使得一切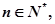 均有
均有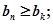
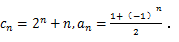 当
当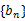 的通项公式.
的通项公式. 粤公网安备 44130202000953号
粤公网安备 44130202000953号