(本小题满分13分)设集合 由满足下列两个条件的数列
由满足下列两个条件的数列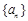 构成:
构成:
①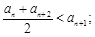 ②存在实数
②存在实数 ,使
,使 .(
.(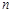 为正整数)
为正整数)
(Ⅰ)在只有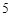 项的有限数列
项的有限数列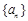 ,
,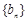 中,其中
中,其中 ,
,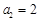 ,
,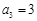 ,
,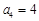 ,
,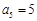 ,
, ,
,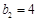 ,
, ,
,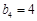 ,
,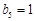 ,试判断数列
,试判断数列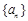 ,
,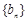 是否为集合
是否为集合 的元素;
的元素;
(Ⅱ)设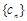 是等差数列,
是等差数列, 是其前
是其前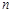 项和,
项和,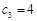 ,
,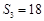 ,证明数列
,证明数列 ;并求出
;并求出 的取值范围.
的取值范围.
相关知识点
推荐套卷
(本小题满分13分)设集合 由满足下列两个条件的数列
由满足下列两个条件的数列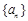 构成:
构成:
①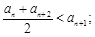 ②存在实数
②存在实数 ,使
,使 .(
.(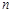 为正整数)
为正整数)
(Ⅰ)在只有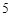 项的有限数列
项的有限数列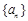 ,
,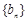 中,其中
中,其中 ,
,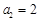 ,
,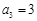 ,
,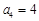 ,
,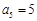 ,
, ,
,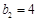 ,
, ,
,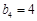 ,
,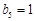 ,试判断数列
,试判断数列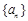 ,
,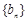 是否为集合
是否为集合 的元素;
的元素;
(Ⅱ)设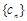 是等差数列,
是等差数列, 是其前
是其前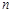 项和,
项和,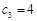 ,
,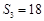 ,证明数列
,证明数列 ;并求出
;并求出 的取值范围.
的取值范围.