高中数学等比数列试题

已知数列 $\left\{a_n\right\}$ ， $a_1=3$ ，前 $n$ 项和为 $S_n$ ．

（1）若 $\left\{a_n\right\}$ 为等差数列，且 $a_4=15$ ，求 $S_n$ ；

（2）若 $\left\{a_n\right\}$ 为等比数列，且 $\underset{x\to \infty }{\lim }{s}_n<12$ ，求公比 $q$ 的取值范围．

设 $\left\{a_n\right\}$是等差数列， $\left\{b_n\right\}$是等比数列．已知 $a_1=4,b_1=6，b_2=2a_2-2,b_3=2a_3+4$．

（Ⅰ）求 $\left\{a_n\right\}$和 $\left\{b_n\right\}$的通项公式；

（Ⅱ）设数列 $\left\{c_n\right\}$满足 $c_1=1,c_n=\left\{\begin{array}{c}1,2^k<n<2^{k+1},\\ b_k,n=2^k,\end{array}\right.$其中 $k\in N^{*}$．

（i）求数列 $\left\{a_{2^n}\left(c_{2^n}-1\right)\right\}$的通项公式；

（ii）求 $\sum _{i=1}^{2^n}{a}_i{c}_i\left(n\in N^{*}\right)$．

已知 $\left\{x_n\right\}$ 是各项均为正数的等比数列，且 $x_1+x_2=3$ ， $x_3﹣x_2=2$ ．

（Ⅰ）求数列 $\left\{x_n\right\}$ 的通项公式；

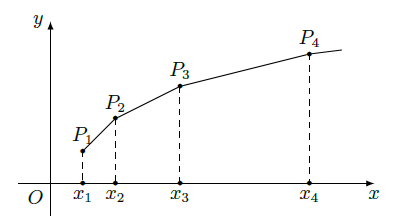
（Ⅱ）如图，在平面直角坐标系 $\mathit{xOy}$ 中，依次连接点 $P_1（x_1\mathit{}，1）$ ， $P_2（x_2\mathit{}，2）\dots P_{n+1}（x_{n+1}\mathit{}，\mathit{n}+1）$ 得到折线 $P1\mathit{P}2\dots P_{n+1}\mathit{}$ ， 求由该折线与直线 $y=0$ ， $x=x_1\mathit{}$ ， $\mathit{x}=x_{n+1}$ 所围成的区域的面积 $T_n$ ．

定义首项为1且公比为正数的等比数列为"M－数列".

（1）已知等比数列{ a _n} $(n\in N^{*})$ 满足： $a_2{a}_4=a_5,a_3-4a_2+4a_4=0$ ，求证:数列{ a _n}为"M－数列"；

（2）已知数列{ b _n}满足: $b_1=1,\frac{1}{S_n}=\frac{2}{b_n}-\frac{2}{b_{n+1}}$ ，其中 S _n为数列{ b _n}的前 n项和．

①求数列{ b _n}的通项公式；

②设 m为正整数，若存在"M－数列"{ c _n} $(n\in N^{*})$ ，对任意正整数 k ，当 k≤ m时，都有 $c_k⩽b_k⩽c_{k+1}$ 成立，求 m的最大值．

在数列{a_n}中，a₁=1，a_n+1=2a_n+2ⁿ．
（1）设b_n=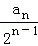，证明：数列{bn}是等差数列；
（2）求数列{a_n}的前n项和S_n，
（3）设c_n=，求数列{c_n}的最大项．

已知等差数列{a_n}的前n项和为S_n，且满足a₂=4，a₃+a₄=17．
（1）求{a_n}的通项公式；
（2）设b_n=2^an+2，证明数列{b_n}是等比数列并求其前n项和T_n．

两个数4和9的等比中项是（）

A．

6

B．

±6

C．

$\frac{13}{2}$

D．

$\pm \frac{13}{2}$

设{a_n}是公比为q的等比数列．
（Ⅰ）推导{a_n}的前n项和S_n公式；
（Ⅱ）设q≠1，证明数列不是等比数列．

设f_n（x）是等比数列1，x，x²，…，xⁿ的各项和，则f_n（2）等于（）

A．2^n﹣1

B．2^n+1﹣1

C．2^n﹣2

D．2^n+1﹣2

已知各项均为正数的数列{a_n}中，a₁=1，S_n是数列{a_n}的前n项和，对任意n∈N^*，有 2S_n=2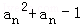．函数f（x）=x²+x，数列{b_n}的首项b₁=．
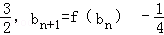（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）令求证：{c_n}是等比数列并求{c_n}通项公式；
（Ⅲ）令d_n=a_n•c_n，（n为正整数），求数列{d_n}的前n项和T_n．

设数列{a_n}是以3为首项，1为公差的等差数列，{b_n}是以1为首项，2为公比的等比数列，则b_a1+b_a2+b_a3+b_a4=（）

A．15

B．60

C．63

D．72

已知正项等比数列{a_n}，且a₂a₁₀=2a₅²，a₃=1，则a₄=（）

A．

B．

C．

D．2

已知在等比数列中，，9，则（）

A．

B．5

C．

D．3

已知为等比数列，，则 ．

在等比数列{a_n}中，a₂＝3，a₅＝81．
（1）求a_n；
（2）设b_n＝log₃a_n，求数列{b_n}的前n项和S_n．