暖春三月,贴心开学测 高三数学第一套
将二项式 的展开式按
的展开式按 的降幂排列,若前三项系数成等差数列,则该展开式中
的降幂排列,若前三项系数成等差数列,则该展开式中 的指数是整数的项共有( )个
的指数是整数的项共有( )个
| A.3 | B.4 | C.5 | D.6 |
函数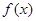 的定义域为
的定义域为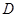 ,若满足:
,若满足:
①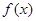 在
在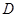 内是单调函数;
内是单调函数;
②存在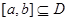 ,使
,使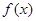 在
在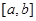 上的值域为
上的值域为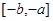 ,那么
,那么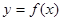 叫做对称函数.
叫做对称函数.
现有 是对称函数,那么
是对称函数,那么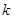 的取值范围是( )
的取值范围是( )
A.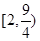 |
B.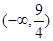 |
C.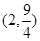 |
D.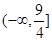 |
给出以下四个命题:
①已知命题 ;命题
;命题 .则命题
.则命题 和
和 都是真命题;
都是真命题;
②过点 且在
且在 轴和
轴和 轴上的截距相等的直线方程是
轴上的截距相等的直线方程是 ;
;
③函数 在定义域内有且只有一个零点;
在定义域内有且只有一个零点;
④先将函数 的图像向右平移
的图像向右平移 个单位,再将新函数的周期扩大为原来的两倍,则所得图像的函数解析式为
个单位,再将新函数的周期扩大为原来的两倍,则所得图像的函数解析式为 .
.
其中正确命题的序号为 .(把你认为正确的命题序号都填上)
(本小题满分12分)如图,三角形 和梯形
和梯形 所在的平面互相垂直,
所在的平面互相垂直,  ,
, ,
, 是线段
是线段 上一点,
上一点, .
.
(Ⅰ)当 时,求证:
时,求证: 平面
平面 ;
;
(Ⅱ)求二面角 的正弦值;
的正弦值;
(Ⅲ)是否存在点 满足
满足 平面
平面 ?并说明理由.
?并说明理由.
(本小题满分12分)某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告费支出为10百万元时,销售额多大?
(可能用到的公式: ,
,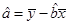 ,其中
,其中 、
、 是对回归直线方程
是对回归直线方程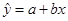 中系数
中系数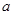 、
、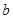 按最小二乘法求得的估计值)
按最小二乘法求得的估计值)
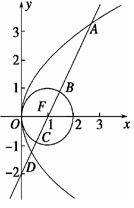
(本小题满分12分)已知抛物线 ,圆
,圆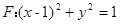 ,过点
,过点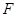 作直线
作直线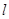 ,自上而下依次与上述两曲线交于点
,自上而下依次与上述两曲线交于点 (如图所示),
(如图所示),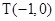 .
.
(Ⅰ)求 ;
;
(Ⅱ)作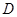 关于
关于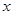 轴的对称点
轴的对称点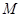 ,求证:
,求证: 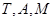 三点共线;
三点共线;
(Ⅲ)作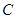 关于
关于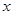 轴的对称点
轴的对称点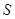 ,求
,求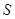 到直线
到直线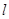 的距离的最大值.
的距离的最大值.
(本小题满分12分)已知函数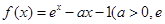 为自然对数的底数)
为自然对数的底数)
(1)求函数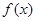 的最小值;
的最小值;
(2)若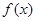 ≥0对任意的x∈R恒成立,求实数a的值;
≥0对任意的x∈R恒成立,求实数a的值;
(3)在(2)的条件下,证明: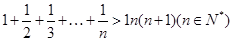
(本小题满分10)选修4—1:几何证明选讲
如图,⊙O内切于△ABC的边于D,E,F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G.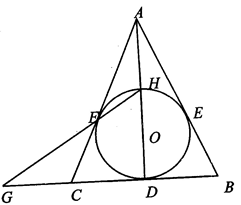
(1)求证:圆心O在直线AD上;
(2)求证:点C是线段GD的中点.
(本小题满分10)选修4-4:坐标系与参数方程
在直角坐标系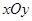 中,已知曲线
中,已知曲线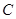 的参数方程是
的参数方程是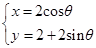 (
(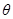 为参数).在极坐标系(与直角坐标系
为参数).在极坐标系(与直角坐标系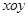 取相同的长度单位,且以原点
取相同的长度单位,且以原点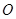 为极点,以
为极点,以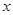 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线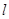 的极坐标方程是
的极坐标方程是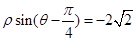 .
.
(Ⅰ)求曲线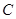 的普通方程和直线
的普通方程和直线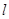 的直角坐标方程;
的直角坐标方程;
(Ⅱ)点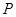 是曲线
是曲线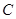 上的动点,求点
上的动点,求点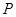 到直线
到直线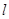 距离的最小值.
距离的最小值.

 ,集合
,集合 ,集合
,集合 ,则
,则 ( )
( )



 为纯虚数,若
为纯虚数,若 (
( 为虚数单位),则实数
为虚数单位),则实数 的值为( )
的值为( )


 是第二象限角,且
是第二象限角,且 ,则
,则 的值为( )
的值为( )



 中,
中, ,点M在边AB上,且满足
,点M在边AB上,且满足 ,则
,则 ( )
( )


 满足
满足 ,
, ,其中
,其中 是等差数列,且
是等差数列,且 ,则
,则 ( )
( )



 ,若
,若 是
是 的最小值,则
的最小值,则 的取值范围为( )
的取值范围为( )




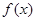 是奇函数,当
是奇函数,当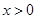 时,
时, ,且
,且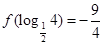 ,则
,则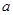 的值为( )
的值为( )
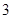
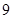
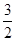
 的一条渐近线与圆
的一条渐近线与圆 相变于A.B两点,若
相变于A.B两点,若 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( ) C.3 D.4
C.3 D.4 满足约束条件
满足约束条件 若
若 取得最大值的最优解不唯一,则实数
取得最大值的最优解不唯一,则实数 的值为( )
的值为( ) 或
或
 或
或
 或
或



 的值域为
的值域为  对任意的
对任意的 有
有 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围 .
. 的前
的前 项和为
项和为 ,且
,且 ,
,
 的通项公式
的通项公式 ,求数列
,求数列
 的最小值为
的最小值为 .
. 时,求
时,求 的最小值.
的最小值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号