已知椭圆C: 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线 与以椭圆C的右焦点为圆心,以
与以椭圆C的右焦点为圆心,以
 为半径的圆相切.
为半径的圆相切.
(1)求椭圆的方程.
(2)若过椭圆 的右焦点
的右焦点 作直线
作直线 交椭圆
交椭圆 于
于 两点,交y轴于
两点,交y轴于 点,且
点,且 求证:
求证: 为定值
为定值
已知函数 .
.
(1)若函数 在
在 处取极值,求
处取极值,求 的值;
的值;
(2)如图,设直线 将坐标平面分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个区域(不含边界),若函数
将坐标平面分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个区域(不含边界),若函数 的图象恰好位于其中一个区域内,判断其所在的区域并求对应的
的图象恰好位于其中一个区域内,判断其所在的区域并求对应的 的取值范围;
的取值范围;
(3)比较 与
与 的大小,并说明理由.
的大小,并说明理由.
(本小题满分10分)(选修4-4极坐标与参数方程选讲)
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.圆C1,直线C2的极坐标方程分别为 ,
, =
= .
.
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点.已知直线PQ的参数方程为 (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.
(本小题满分14分)已知函数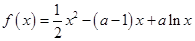 ,其中常数
,其中常数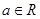 .
.
(Ⅰ)当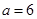 时,求函数
时,求函数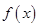 的极值点;
的极值点;
(Ⅱ)证明:对任意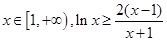 恒成立;
恒成立;
(Ⅲ)对于函数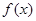 图象上的不同两点
图象上的不同两点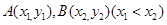 ,如果在函数
,如果在函数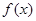 图象上存在点
图象上存在点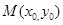 (其中
(其中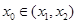 ),使得在点M处的切线
),使得在点M处的切线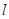 ∥AB,则称直线AB存在“伴侣切线”.特别地,当
∥AB,则称直线AB存在“伴侣切线”.特别地,当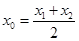 ,又称直线AB存在“中值伴侣切线”.
,又称直线AB存在“中值伴侣切线”.
试问:当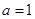 时,对于函数
时,对于函数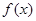 图象上不同两点A、B,直线AB是否存在“中值伴侣切线”,并证明你的结论.
图象上不同两点A、B,直线AB是否存在“中值伴侣切线”,并证明你的结论.
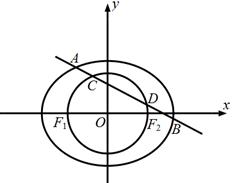
(本小题满分12分)已知椭圆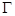 :
: (
(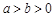 )的长半轴长为2,离心率为
)的长半轴长为2,离心率为 ,左右焦点分别为
,左右焦点分别为 ,
, .
.
(Ⅰ)求椭圆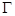 的方程;
的方程;
(Ⅱ)若直线 与椭圆
与椭圆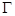 交于
交于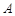 ,
,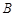 两点,与以
两点,与以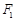 ,
, 为直径的圆交于
为直径的圆交于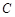 ,
,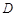 两点,且满足
两点,且满足 ,求直线
,求直线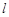 的方程.
的方程.
(本小题满分14分)设曲线 在点
在点 处的切线斜率为
处的切线斜率为 ,且
,且 。对一切实数
。对一切实数 ,不等式
,不等式 恒成立
恒成立
(Ⅰ)求 的值。
的值。
(Ⅱ)求函数 的表达式;
的表达式;
(Ⅲ)求证:
(本小题满分16分)已知函数 的图象上,以N(1,n)为切点的切线的倾斜角为
的图象上,以N(1,n)为切点的切线的倾斜角为 .
.
(1)求m,n的值;
(2)是否存在最小的正整数k,使得不等式 ≤k-1991对于
≤k-1991对于 恒成立;
恒成立;
(3)求证: ≤
≤ .
.
(本小题满分14分)已知函数 ,若函数
,若函数 在点
在点 处的切线与直线
处的切线与直线 相互垂直.
相互垂直.
(1)求 的值.
的值.
(2)求函数 的最大值.
的最大值.
(3)证明:对于任意的 ,都有
,都有 成立.
成立.
已知函数 .
.
(Ⅰ)若 不等式
不等式 的解集为
的解集为 ,
, ,求
,求 的取值范围;
的取值范围;
(Ⅱ)若 为整数,
为整数, ,且函数
,且函数 在
在 上恰有一个零点,求
上恰有一个零点,求 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下,若函数 对任意的x∈
对任意的x∈ ,有
,有 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
已知函数 .
.
(Ⅰ)若 不等式
不等式 的解集为
的解集为 ,
, ,求
,求 的取值范围;
的取值范围;
(Ⅱ)若 为整数,
为整数, ,且函数
,且函数 在
在 上恰有一个零点,求
上恰有一个零点,求 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下,若函数 对任意的x∈
对任意的x∈ ,有
,有 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.