已知圆C:(x-1)2+(y-1)2=2经过椭圆Γ∶ (a>b>0)的右焦点F和上顶点B.
(a>b>0)的右焦点F和上顶点B.
(1)求椭圆Γ的方程;
(2)如图,过原点O的射线l与椭圆Γ在第一象限的交点为Q,与圆C的交点为P,M为OP的中点, 求 的最大值.
的最大值.
(本小题满分13分)已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,椭圆上的点
,椭圆上的点 满足
满足 ,且
,且 的面积为
的面积为 .
.
(1)求椭圆C的方程;
(2)设椭圆 的左、右顶点分别为
的左、右顶点分别为 ,过点
,过点 的动直线
的动直线 与椭圆
与椭圆 相交于
相交于 两点,直线
两点,直线 与直线
与直线 的交点为
的交点为 ,证明:点
,证明:点 总在直线
总在直线 上.
上.
(本小题满分13分)
设数列 的前
的前 项和为
项和为 ,若对任意的正整数
,若对任意的正整数 ,总存在正整数
,总存在正整数 ,使得
,使得 ,则称
,则称 是“
是“ 数列”。
数列”。
(1)若数列 的前
的前 项和为
项和为 ,证明:
,证明: 是“
是“ 数列”;
数列”;
(2)设 是等差数列,其首项
是等差数列,其首项 ,公差
,公差 ,若
,若 是“
是“ 数列”,求
数列”,求 的值;
的值;
(3)证明:对任意的等差数列 ,总存在两个“
,总存在两个“ 数列”
数列” ,使得
,使得 成立。
成立。
(本小题满分14分)
(1)若 是
是 的一个极值点,求
的一个极值点,求 的单调区间;
的单调区间;
(2)证明:若 ;
;
(3)证明:若 .
.
已知数列{an}中,a1= ,an+1=
,an+1= (n∈N*).
(n∈N*).
(1)求证:数列{ }是等差数列,并求{an}的通项公式;
}是等差数列,并求{an}的通项公式;
(2)设bn+an=l(n∈N*),S=b1b2+b2b3+…+bnbn+1,试比较an与8Sn的大小.
(本题12分)已知二次函数 满足条件
满足条件 ,且方程
,且方程 有两个相等的实根,求
有两个相等的实根,求 的解析式和值域.
的解析式和值域.
(本小题满分14分)已知 ,
, ,
, ,其中
,其中 .
.
(1)若 与
与 的图像在交点
的图像在交点 处的切线互相垂直,求
处的切线互相垂直,求 的值;
的值;
(2)若 是函数
是函数 的一个极值点,
的一个极值点, 和
和 是
是 的两个零点,且
的两个零点,且  ,
, ,求
,求 的值;
的值;
(3)当 时,若
时,若 ,
, 是
是 的两个极值点,当
的两个极值点,当 时,求证:
时,求证: .
.
(本小题满分13分)设F1,F2分别是椭圆 的左右焦点.
的左右焦点.
(1)若P是该椭圆上的一个动点,求 的最大值和最小值.
的最大值和最小值.
(2)是否存在经过点A(5,0)的直线l与椭圆交于不同的两点C,D,使得|F2C|=|F2D|?若存在,求直线l的方程;若不存在,请说明理由.
设椭圆E中心在原点,焦点在x轴上,短轴长为4,点Q(2, )在椭圆上.
)在椭圆上.
(1)求椭圆E的方程;
(2)设动直线L交椭圆E于A、B两点,且 ,求△OAB的面积的取值范围.
,求△OAB的面积的取值范围.
(3)过M( )的直线
)的直线 :
: 与过N(
与过N( )的直线
)的直线 :
: 的交点P(
的交点P( )在椭圆E上,直线MN与椭圆E的两准线分别交于G,H两点,求
)在椭圆E上,直线MN与椭圆E的两准线分别交于G,H两点,求 ·
· 的值.
的值.
已知椭圆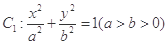 过点
过点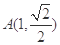 ,其焦距为
,其焦距为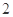 .
.
(1)求椭圆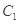 的方程;
的方程;
(2)已知椭圆具有如下性质:若椭圆的方程为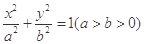 ,则椭圆在其上一点
,则椭圆在其上一点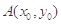 处的切线方程为
处的切线方程为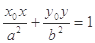 ,试运用该性质解决以下问题:
,试运用该性质解决以下问题:
(i)如图(1),点 为
为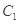 在第一象限中的任意一点,过
在第一象限中的任意一点,过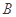 作
作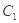 的切线
的切线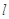 ,
,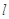 分别与
分别与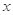 轴和
轴和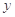 轴的正半轴交于
轴的正半轴交于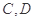 两点,求
两点,求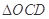 面积的最小值;
面积的最小值;
(ii)如图(2),过椭圆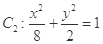 上任意一点
上任意一点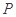 作
作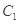 的两条切线
的两条切线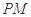 和
和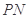 ,切点分别为
,切点分别为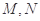 .当点
.当点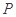 在椭圆
在椭圆 上运动时,是否存在定圆恒与直线
上运动时,是否存在定圆恒与直线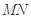 相切?若存在,求出圆的方程;若不存在,请说明理由.
相切?若存在,求出圆的方程;若不存在,请说明理由.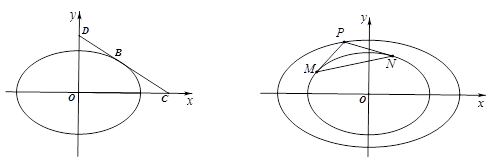
图(1) 图(2)