(本小题满分13分)
设数列 的前
的前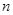 项和为
项和为 ,若对任意的正整数
,若对任意的正整数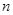 ,总存在正整数
,总存在正整数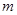 ,使得
,使得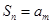 ,则称
,则称 是“
是“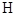 数列”。
数列”。
(1)若数列 的前
的前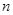 项和为
项和为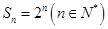 ,证明:
,证明: 是“
是“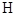 数列”;
数列”;
(2)设 是等差数列,其首项
是等差数列,其首项 ,公差
,公差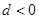 ,若
,若 是“
是“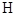 数列”,求
数列”,求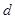 的值;
的值;
(3)证明:对任意的等差数列 ,总存在两个“
,总存在两个“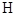 数列”
数列” ,使得
,使得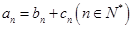 成立。
成立。
相关知识点
推荐套卷
(本小题满分13分)
设数列 的前
的前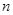 项和为
项和为 ,若对任意的正整数
,若对任意的正整数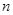 ,总存在正整数
,总存在正整数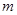 ,使得
,使得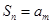 ,则称
,则称 是“
是“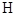 数列”。
数列”。
(1)若数列 的前
的前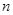 项和为
项和为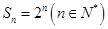 ,证明:
,证明: 是“
是“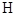 数列”;
数列”;
(2)设 是等差数列,其首项
是等差数列,其首项 ,公差
,公差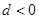 ,若
,若 是“
是“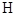 数列”,求
数列”,求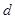 的值;
的值;
(3)证明:对任意的等差数列 ,总存在两个“
,总存在两个“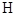 数列”
数列” ,使得
,使得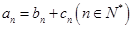 成立。
成立。