如图1：等边
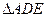可以看作由等边
绕顶点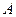
经过旋转相似变换得到.但是我们注意到图形中的
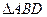和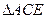
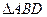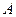的关系，上述变换也可以理解为图形是由绕顶点旋转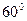
形成的.于是我们得到一个结论：如果两个正三角形存在着公共顶点，则该图形可以看成是由一个三角形绕着该顶点旋转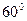形成的.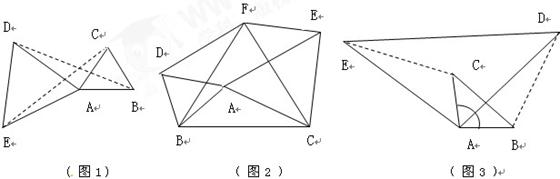
① 利用上述结论解决问题：如图2，中，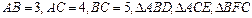
都是等边三角形，求四边形
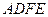的面积;
② 图3中, ∽，
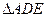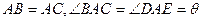，仿照上述结论,推广出符合图3的结论.（写出结论即可）
相关试题
首项
，前
项和
与
之间满足
.
是等差数列；
，使
对
都成立，求
中，
.
满足
，设
，且
，求
的值.
满足
，
，
.
的前
项和
；
中，
是其前
项和，且
成等比数列.
；
，求等差数列
各项为正数，
是其前
项和，且
.
及推荐套卷
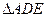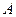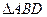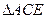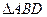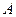如图1：等边可以看作由等边绕顶点经过旋转相似变换得到.但是我们注意到图形中的和的关系，上述变换也可以理解为图形是由绕顶点旋转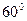形成的.于是我们得到一个结论：如果两个正三角形存在着公共顶点，则该图形可以看成是由一个三角形绕着该顶点旋转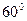形成的.
① 利用上述结论解决问题：如图2，中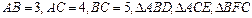，都是等边三角形，求四边形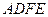的面积;
② 图3中, ∽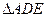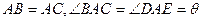，，仿照上述结论,推广出符合图3的结论.（写出结论即可）
粤公网安备 44130202000953号