(本小题15分)设动点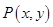
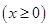 到定点
到定点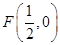 的距离比到
的距离比到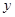 轴的距离大
轴的距离大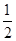 .记点
.记点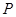 的轨迹为曲线C.
的轨迹为曲线C.
(1)求点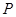 的轨迹方程;
的轨迹方程;
(2)设圆M过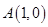 ,且圆心M在P的轨迹上,
,且圆心M在P的轨迹上,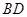 是圆M在
是圆M在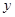 轴上截得的弦,当圆心M运动时弦长
轴上截得的弦,当圆心M运动时弦长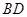 是否为定值?说明理由;
是否为定值?说明理由;
(3)过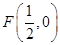 作互相垂直的两直线交曲线C于G、H、R、S,求四边形
作互相垂直的两直线交曲线C于G、H、R、S,求四边形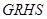 面积的最小值.
面积的最小值.
相关知识点
推荐套卷
(本小题15分)设动点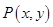
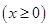 到定点
到定点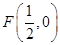 的距离比到
的距离比到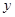 轴的距离大
轴的距离大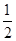 .记点
.记点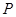 的轨迹为曲线C.
的轨迹为曲线C.
(1)求点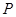 的轨迹方程;
的轨迹方程;
(2)设圆M过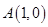 ,且圆心M在P的轨迹上,
,且圆心M在P的轨迹上,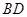 是圆M在
是圆M在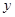 轴上截得的弦,当圆心M运动时弦长
轴上截得的弦,当圆心M运动时弦长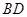 是否为定值?说明理由;
是否为定值?说明理由;
(3)过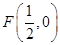 作互相垂直的两直线交曲线C于G、H、R、S,求四边形
作互相垂直的两直线交曲线C于G、H、R、S,求四边形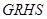 面积的最小值.
面积的最小值.