(本小题满分13分)已知椭圆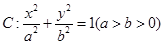 的左、右焦点分别为
的左、右焦点分别为 ,椭圆上的点
,椭圆上的点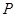 满足
满足 ,且
,且 的面积为
的面积为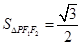 .
.
(1)求椭圆C的方程;
(2)设椭圆 的左、右顶点分别为
的左、右顶点分别为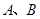 ,过点
,过点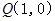 的动直线
的动直线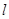 与椭圆
与椭圆 相交于
相交于 两点,直线
两点,直线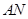 与直线
与直线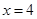 的交点为
的交点为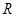 ,证明:点
,证明:点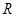 总在直线
总在直线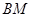 上.
上.
推荐套卷
(本小题满分13分)已知椭圆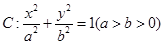 的左、右焦点分别为
的左、右焦点分别为 ,椭圆上的点
,椭圆上的点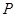 满足
满足 ,且
,且 的面积为
的面积为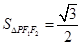 .
.
(1)求椭圆C的方程;
(2)设椭圆 的左、右顶点分别为
的左、右顶点分别为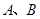 ,过点
,过点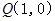 的动直线
的动直线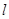 与椭圆
与椭圆 相交于
相交于 两点,直线
两点,直线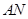 与直线
与直线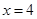 的交点为
的交点为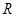 ,证明:点
,证明:点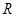 总在直线
总在直线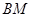 上.
上.