暖春三月,贴心开学测 高一数学第六套
已知某几何体的俯视图是如图所示的边长为2的正方形,主视图与左视图是边长为2的正三角形,则其全面积是( )

| A.8 | B.12 | C. |
D. |
来源:暖春三月,贴心开学测 高一数学第六套
如图,PA垂直于圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E, F分别是点A在P B, P C上的射影,给出下列结论:
① ;②
;② ;③
;③ ;④
;④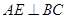 .正确命题的个数为( )
.正确命题的个数为( )
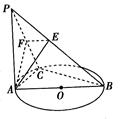
| A.1 | B.2 | C.3 | D.4 |
来源:暖春三月,贴心开学测 高一数学第六套
关于函数 ,给出下列四个命题:
,给出下列四个命题:
① ,
, 时,
时, 只有一个实数根;
只有一个实数根;
② 时,
时, 是奇函数;
是奇函数;
③ 的图象关于点
的图象关于点 ,
, 对称;
对称;
④函数 至多有两个零点.
至多有两个零点.
其中正确的命题序号为______________.
来源:暖春三月,贴心开学测 高一数学第六套
(本小题满分10分)设不等式 的解集为集合
的解集为集合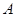 ,关于
,关于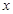 的不等式
的不等式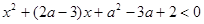 的解集为集合
的解集为集合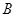 .
.
(1)若 ,求实数
,求实数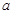 的取值范围;
的取值范围;
(2)若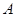 ∩
∩ ,求实数
,求实数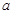 的取值范围.
的取值范围.
来源:暖春三月,贴心开学测 高一数学第六套
(本小题满分12分)已知圆 ,
,
(1)若直线 过定点
过定点 (1,0),且与圆
(1,0),且与圆 相切,求
相切,求 的方程;
的方程;
(2)若圆 的半径为3,圆心在直线
的半径为3,圆心在直线 :
: 上,且与圆
上,且与圆 外切,求圆
外切,求圆 的方程.
的方程.
来源:暖春三月,贴心开学测 高一数学第六套
(本小题满分12分)过点 的圆C与直线
的圆C与直线 相切于点A(4,0).
相切于点A(4,0).
(1)求圆C的方程;
(2)已知点 的坐标为
的坐标为 ,设
,设 分别是直线
分别是直线 和圆
和圆 上的动点,求
上的动点,求 的最小值.
的最小值.
(3)在圆C上是否存在两点 关于直线
关于直线 对称,且以
对称,且以 为直径的圆经过原点?若存在,写出直线
为直径的圆经过原点?若存在,写出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
来源:暖春三月,贴心开学测 高一数学第六套
 ,集合
,集合 ,则
,则 为( )
为( )



 ,则
,则 ( )
( )



 是两条不同的直线,
是两条不同的直线, 是个平面,则下列命题正确的是( )
是个平面,则下列命题正确的是( ) ,则
,则
 ,则
,则
 ,则
,则
 ,则
,则




 的零点所在的一个区间是( )
的零点所在的一个区间是( )


 与圆
与圆 有公共点,则实数
有公共点,则实数 取值范围是( )
取值范围是( )



 ,
,  ,
,  ,
,  ,则( )
,则( )



 的直线与圆
的直线与圆 相交于
相交于 ,
, 两点,则
两点,则 的最小值为( )
的最小值为( )

 为定义在
为定义在 上的奇函数,当
上的奇函数,当 时,
时, (
( 为常数),则
为常数),则 ( )
( )



 ,
, ,直线
,直线 过点
过点 且与线段
且与线段 相交,则直线
相交,则直线 的取值范围是( )
的取值范围是( ) 或
或



 且与直线
且与直线 平行的直线方程是______________.
平行的直线方程是______________.  的单调增区间为 .
的单调增区间为 . 中,
中,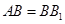 ,
, ,
,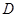 为的
为的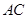 中点.
中点.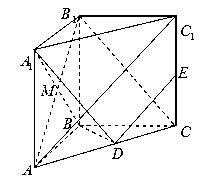
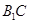 ∥平面
∥平面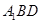 ;
; 平面
平面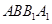 ;
; 中,D、E分别是
中,D、E分别是 、
、 的中点,
的中点,  .
.
 ;
; 的体积.
的体积. 满足
满足 ,对任意
,对任意 都有
都有 ,且
,且 .
. 的解析式;
的解析式; ,使函数
,使函数 在
在 上为减函数?若存在,求出实数
上为减函数?若存在,求出实数 粤公网安备 44130202000953号
粤公网安备 44130202000953号