高中数学不定方程和方程组解答题

（本小题满分12分）已知函数，（）．
（Ⅰ）求函数的递增区间；
（Ⅱ）若函数在上有两个不同的零点、，求的值．

如图是一个半圆形湖面景点的平面示意图．已知为直径，且km,为圆心，为圆周上靠近 的一点，为圆周上靠近 的一点，且∥．现在准备从经过到建造一条观光路线，其中到是圆弧，到是线段.设，观光路线总长为.

（1）求关于的函数解析式，并指出该函数的定义域；
（2）求观光路线总长的最大值.

（本小题满分12分）已知函数
（1）当时，如果函数仅有一个零点，求实数的取值范围；
（2）当时，试比较与1的大小；
（3）求证：

已知，函数．
（Ⅰ）当时，求函数的最小值；
（Ⅱ）当时，讨论的图象与的图象的公共点个数．

（本题满分14分，第1小题6分，第2小题8分）
已知函数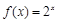的反函数为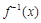
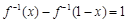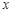（1）若，求实数的值；
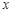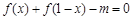（2）若关于的方程在区间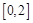内有解，求实数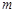的取值范围；

（本小题满分12分，（Ⅰ）小问2分，（Ⅱ）小问3分，（Ⅲ）小问5分）
已知a，b，c，d是不全为零的实数，函数，，方程
的实根都是的实根；反之，方程的实根都是的实根．
（Ⅰ）求d的值；
（Ⅱ）若，求c的取值范围；
（Ⅲ）若，，求c的取值范围．

已知函数，现将的图像向右平移一个单位，再向上平移一个单位得到函数的图像．
（1）求函数的解析式；
（2）函数的图像与函数的图像在上至少有一个交点，求实数的取值范围．

已知函数 $f\left(x\right)=x^3+a{x}^2+b(a,b\in R)$.
（1）试讨论 $f\left(x\right)$的单调性；
（2）若 $b=c-a$（实数 $c$是 $a$与无关的常数），当函数 $f\left(x\right)$有三个不同的零点时， $a$的取值范围恰好是 $(-\infty ,-3)\cup (1,\frac{3}{2})\cup (\frac{3}{2},+\infty )$，求 $c$的值.

已知二次函数f（x）=ax²+bx+c ．
（1）设集合A={x|f（x）=x}．
①若A={1，2}，且f（0）=2，求f（x）的解析式；
②若A={1}，且a≥1，求f（x）在区间[﹣2，2]上的最大值M（a）．
（2）设f（x）的图像与x轴有两个不同的交点，a>0， f（c）=0，且当0<x<c时，f（x）>0．用反证法证明：．

已知条件使不等式成立；条件有两个负数根，若为真，且为假，求实数的取值范围．

某厂生产某种产品（百台），总成本为（万元），其中固定成本为2万元， 每生产1百台，成本增加1万元，销售收入（万元），假定该产品产销平衡。
（1）若要该厂不亏本，产量应控制在什么范围内？
（2）该厂年产多少台时，可使利润最大？
（3）求该厂利润最大时产品的售价。

我国西部某省4A级风景区内住着一个少数民族村，该村投资了800万元修复和加强民俗文化基础设施，据调查，修复好村民俗文化基础设施后，任何一个月内（每月按30天计算）每天的旅游人数与第x天近似地满足（千人），且参观民俗文化村的游客人均消费近似地满足（元）．
（1）求该村的第x天的旅游收入（单位千元，1≤x≤30，）的函数关系；
（2）若以最低日收入的20％作为每一天的计量依据，并以纯收入的5％的税率收回投资成本，试问该村在两年内能否收回全部投资成本？

设函数 $f\left(x\right)=x^2+ax+b(a,b\in R)$.

（1）当 $b=\frac{a^2}{4}+1$时，求函数 $f\left(x\right)$在 $\left[-1,1\right]$上的最小值 $g\left(a\right)$的表达式；
（2）已知函数 $f\left(x\right)$在 $\left[-1,1\right]$上存在零点， $0\le b-2a\le 1$，求 $b$的取值范围.

（本小题满分16分）
（1）
（2），求的取值范围。
（3）条件．

设，函数，函数，.
（Ⅰ）当时，写出函数零点个数，并说明理由；
（Ⅱ）若曲线与曲线分别位于直线的两侧，求的所有可能取值.