已知二次函数 满足
满足 ,且关于
,且关于 的方程
的方程 的两个实数根分别在区间
的两个实数根分别在区间 、
、 内.
内.
(1)求实数 的取值范围;
的取值范围;
(2)若函数 在区间
在区间 上具有单调性,求实数
上具有单调性,求实数 的取值范围.
的取值范围.
已知函数 .
.
(Ⅰ)当 时,证明:
时,证明: 为奇函数;
为奇函数;
(Ⅱ)若关于 的方程
的方程 有两个不等实数根,求实数
有两个不等实数根,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知函数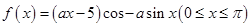 ,其中
,其中 为正实数。
为正实数。
(1)当 时,求
时,求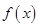 在
在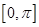 上的零点个数。
上的零点个数。
(2)对于定义域内的任意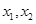 ,将
,将 的最大值记作
的最大值记作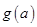 ,求
,求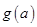 的表达式。
的表达式。
某种商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到 元.公司拟投入
元.公司拟投入 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入 万元作为浮动宣传费用.试问:当该商品明年的销售量
万元作为浮动宣传费用.试问:当该商品明年的销售量 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
已知函数 。
。
(1)若 ,求不等式
,求不等式 的解集;
的解集;
(2)若函数 在
在 上有两个零点
上有两个零点 ,求
,求 的取值范围.
的取值范围.
设已知函数 ,
,
(1)当 时,求函数
时,求函数 的最大值的表达式
的最大值的表达式
(2)是否存在实数 ,使得
,使得 有且仅有3个不等实根,且它们成等差数列,若存在,求出所有
有且仅有3个不等实根,且它们成等差数列,若存在,求出所有 的值,若不存在,说明理由.
的值,若不存在,说明理由.
已知f(x)= .
.
(1)求f(x)的单调区间;
(2)令g(x)=ax2﹣2lnx,则g(x)=1时有两个不同的根,求a的取值范围;
(3)存在x1,x2∈(1,+∞)且x1≠x2,使|f(x1)﹣f(x2)|≥k|lnx1﹣lnx2|成立,求k的取值范围.