高中数学不定方程和方程组解答题

设定义域为的单调函数，对任意，都有，若是方程的一个解，且，则实数=    ．

（本小题14分）设函数,
（1）当时，求函数f（x）的零点；
（2）当时，判断的奇偶性并给予证明；
（3）当时，恒成立，求的最大值．

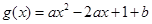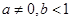已知函数（），在区间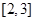上有最大值4，最小值1，设．
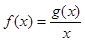（1）求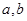的值；
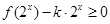（2）不等式在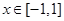上恒成立，求实数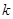的取值范围；
（3）方程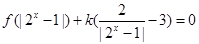有三个不同的实数解，求实数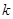的取值范围．

4-5：不等式选讲（本小题满分10分）
已知函数．
（1）若是定义域为的奇函数，试求实数的值；
（2）在（1）的条件下，若函数有三个零点，试求实数的取值范围．

某投资公司计划投资A，B两种金融产品，根据市场调查与预测，A产品的利润与投资量成正比，其关系如图1，B产品的利润与投资量的算术平方根成正比例，其关系如图2，（注：利润与投资量单位：万元）

（1）分别将A，B两产品的利润表示为投资量的函数关系式；
（2）该公司已有10万元资金，并全部投入A，B两种产品中，问：怎样分配这10万元投资，才能使公司获得最大利润？其最大利润为多少万元？

已知函数是定义在上的奇函数．当时，，且图象过点与点.
（Ⅰ）求实数的值，并求函数的解析式；
（Ⅱ）若关于的方程有两个不同的实数解，请写出实数的取值范围；
（Ⅲ）解关于的不等式，写出解集.

设命题：方程无实数根；命题：函数的定义域是．如果命题为真命题，求实数的取值范围．

已知函数是偶函数．
（Ⅰ）求的值；
（Ⅱ）设,若函数与的图象有且只有一个公共点，求实数的取值范围．

已知二次函数f（x）=ax²+bx+1（a，b∈R，a＞0），设方程f（x）=x的两个实数根为x₁和x₂．
（1）如果x₁＜2＜x₂＜4，设二次函数f（x）的对称轴为x=x₀，求证：x₀＞﹣1；
（2）如果|x₁|＜2，|x₂﹣x₁|=2，求b的取值范围．

【原创】设命题p：直线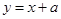与圆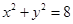有公共点，命题q:关于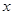的方程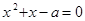的一根大于1，另一根小于1，命题“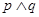”为假命题，命题“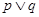”为真命题，求实数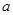的取值范围．

已知命题 成立．命题有实数根．若为假命题，为假命题，求实数的取值范围．

已知函数，设方程有两个实数根
（1）若果，设函数的对称轴为，求证：
（2）如果的两个实数根相差2，求实数b的取值范围。

已知函数，设方程有两个实数根
（1）若果，设函数的对称轴为，求证：
（2）如果的两个实数根相差2，求实数b的取值范围。

已知且，函数，，记
（Ⅰ）求函数的定义域及其零点；
（Ⅱ）若关于的方程在区间内仅有一解，求实数的取值范围．

已知一次函数满足．
（1）求这个函数的解析式；
（2）若函数，求函数的零点．