某种商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到 元.公司拟投入
元.公司拟投入 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入 万元作为浮动宣传费用.试问:当该商品明年的销售量
万元作为浮动宣传费用.试问:当该商品明年的销售量 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
已知函数f(x)= ,曲线
,曲线 在点(0,2)处的切线与
在点(0,2)处的切线与 轴交点的横坐标为-2.
轴交点的横坐标为-2.
(Ⅰ)求a;
(Ⅱ)当 时,曲线
时,曲线 与直线
与直线 只有一个交点,求x的取值范围.
只有一个交点,求x的取值范围.
已知函数
(Ⅰ)当 时,求使
时,求使 成立的
成立的 的值;
的值;
(Ⅱ)当 ,求函数
,求函数 在
在 上的最大值;
上的最大值;
(Ⅲ)对于给定的正数 ,有一个最大的正数
,有一个最大的正数 ,使
,使 时,都有
时,都有 ,试求出这个正数
,试求出这个正数 ,并求它的取值范围.
,并求它的取值范围.
已知二次函数 满足
满足 ,且关于
,且关于 的方程
的方程 的两个实数根分别在区间
的两个实数根分别在区间 、
、 内.
内.
(1)求实数 的取值范围;
的取值范围;
(2)若函数 在区间
在区间 上具有单调性,求实数
上具有单调性,求实数 的取值范围.
的取值范围.
已知函数 .
.
(1)当 时,求
时,求 的零点;
的零点;
(2)若方程 有三个不同的实数解,求
有三个不同的实数解,求 的值;
的值;
(3)求 在
在 上的最小值
上的最小值 .
.
设函数 .
.
(1)若函数 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;
(2)当a=1时,求函数 在区间[t,t+3]上的最大值.
在区间[t,t+3]上的最大值.
)已知函数
(1)若直线 过点
过点 ,并且与曲线
,并且与曲线 相切,求直线
相切,求直线 的方程;
的方程;
(2)设函数 在
在 上有且只有一个零点,求
上有且只有一个零点,求 的取值范围。(其中
的取值范围。(其中 为自然对数的底数)
为自然对数的底数)
(本小题满分12分)已知函数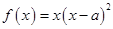 ,
,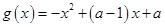 (其中
(其中 ).
).
(Ⅰ)如果函数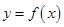 和
和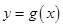 有相同的极值点,求
有相同的极值点,求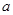 的值,并直接写出函数
的值,并直接写出函数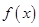 的单调区间;
的单调区间;
(Ⅱ)令 ,讨论函数
,讨论函数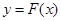 在区间
在区间 上零点的个数。
上零点的个数。
(本小题满分13分)已知函数 ,其中
,其中 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)证明函数 只有一个零点.
只有一个零点.
已知二次函数 满足
满足 (
( ),且
),且 .
.
(1)求 的解析式;
的解析式;
(2)若函数 在区间
在区间 上是单调函数,求实数
上是单调函数,求实数 的取值范围;
的取值范围;
(3)若关于 的方程
的方程 有区间
有区间 上有唯一实数根,求实数
上有唯一实数根,求实数 的取值范围(注:相等的实数根算一个).
的取值范围(注:相等的实数根算一个).
(本小题满分13分)已知函数 .
.
(Ⅰ)当 时,函数
时,函数 恰有3个零点,求实数
恰有3个零点,求实数 的取值范围;
的取值范围;
(Ⅱ)若对任意 ,有
,有 恒成立,求
恒成立,求 的取值范围.
的取值范围.