北京市延庆县高二第二学期期末考试数学(理)试卷
在复平面内,复数 对应的点位于
对应的点位于
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
现有高一学生9人,高二学生12人,高三学生7人,自发组织参加数学课外活动小组,从中推选两名来自不同年级的学生做一次活动的主持人,共有不同的选法
| A.756种 | B.56种 | C.28种 | D.255种 |
若变量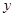 与
与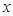 之间的相关系数
之间的相关系数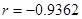 ,则变量
,则变量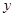 与
与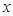 之间
之间
| A.不具有线性相关关系 |
| B.具有线性相关关系 |
| C.它们的线性相关关系还需要进一步确定 |
| D.不确定 |
“指数函数 是增函数,
是增函数, 是指数函数,所以
是指数函数,所以
 是增函数”,在以上演绎推理中,下列说法正确的是
是增函数”,在以上演绎推理中,下列说法正确的是
| A.推理完全正确 | B.大前提不正确 |
| C.小前提不正确 | D.推理形式不正确 |
袋中有大小相同的4个红球,6个白球,每次从中摸取一球,每个球被取到的可能性相同,现不放回地取3个球,则在前两次取出的是白球的前提下,第三次取出红球的概率为
A. |
B. |
C. |
D. |
已知某电子元件的使用寿命(单位:小时)服从正态分布 ,那么该电子元件的使用寿命超过1000小时的概率为 .
,那么该电子元件的使用寿命超过1000小时的概率为 .
用 长的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,则该长方体的最大体积是_____
长的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,则该长方体的最大体积是_____ .
.
(本小题满分10分)
(Ⅰ)证明: .
.
(Ⅱ)已知圆的方程是 ,则经过圆上一点
,则经过圆上一点 的切线方程为
的切线方程为 ,类比上述性质,试写出椭圆
,类比上述性质,试写出椭圆 类似的性质.
类似的性质.
(本小题满分10分)已知函数 在
在 处取得极值.
处取得极值.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)过点 作曲线
作曲线 的切线,求此切线方程.
的切线,求此切线方程.
(本小题满分12分)已知一个袋子中有3个白球和3个红球,这些球除颜色外完全相同.
(Ⅰ)每次从袋中取出一个球,取出后不放回,直到取到一个红球为止,求取球次数 的分布列和数学期望
的分布列和数学期望 ;
;
(Ⅱ)每次从袋中取出一个球,取出后放回接着再取一个球,这样取3次,求取出红球次数 的数学期望
的数学期望 .
.
(本小题满分13分)已知函数 .
.
(Ⅰ)当 时,函数
时,函数 恰有3个零点,求实数
恰有3个零点,求实数 的取值范围;
的取值范围;
(Ⅱ)若对任意 ,有
,有 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分12分)某项选拔共有四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被淘汰.已知某选手能正确回答第一、二、三、四轮问题的概率依次为 ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手进入第四轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率.
 相切的一条直线方程为
相切的一条直线方程为








 ,直线
,直线 及
及 轴所围成的图形的面积为
轴所围成的图形的面积为

 ,(
,( 为参数)上与点
为参数)上与点 的距离等于
的距离等于 的点的坐标是
的点的坐标是
 或
或

 是奇函数
是奇函数 的导函数,
的导函数, ,当
,当 时,
时, ,则使得
,则使得 成立的
成立的 的取值范围是
的取值范围是



 展开式中的常数项是 .
展开式中的常数项是 . ,则
,则 在点
在点 处的线方程为 .
处的线方程为 . 表示取到次品的件数,则
表示取到次品的件数,则 .
. ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, , ,则第
, ,则第 个数对是 .
个数对是 . ,
, ,其中
,其中 ,
, 为自然对数的底数.
为自然对数的底数. 在
在 上的最小值;
上的最小值; ,使得
,使得 在区间
在区间 粤公网安备 44130202000953号
粤公网安备 44130202000953号