:已知函数 ,
,
(1)若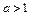 ,且关于
,且关于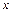 的方程
的方程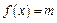 有两个不同的正数解,求实数
有两个不同的正数解,求实数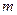 的取值范围;
的取值范围;
(2)设函数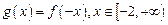 ,
,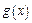 满足如下性质:若存在最大(小)值,则最大(小)值与
满足如下性质:若存在最大(小)值,则最大(小)值与 无关.试求
无关.试求 的取值范围.
的取值范围.
(本小题满分14分)
已知函数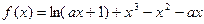 .
.
(Ⅰ)若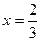 为
为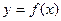 的极值点,求实数
的极值点,求实数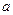 的值;
的值;
(Ⅱ)若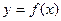 在
在 上为增函数,求实数
上为增函数,求实数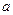 的取值范围;
的取值范围;
(Ⅲ)若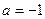 时,方程
时,方程 有实根,求实数
有实根,求实数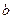 的取值范围.
的取值范围.
已知定义在R上的奇函数  满足
满足  ,且
,且  时,
时, ,给出下列结论:
,给出下列结论:
① ; ②函数
; ②函数 在
在  上是增函数;
上是增函数;
③函数 的图像关于直线x=1对称;
的图像关于直线x=1对称;
④若  ,则关于x的方程
,则关于x的方程 在[-8,16]上的所有根之和为12.
在[-8,16]上的所有根之和为12.
则其中正确的命题为_________.
在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600无后,逐步偿还转让费(不计息).在甲提供的资料中有:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需要各种开支2 000元.
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
已知二次函数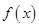 的最小值为
的最小值为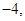 且关于
且关于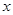 的不等式
的不等式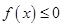 的解集为
的解集为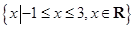 ,
,
(1)求函数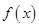 的解析式;
的解析式;
(2)求函数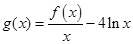 的零点个数.
的零点个数.
(本小题满分15分)函数 ,
,
(1)若 ,试讨论函数
,试讨论函数 的单调性;
的单调性;
(2)若 ,试讨论
,试讨论 的零点的个数;
的零点的个数;