已知定义在R上的奇函数 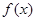 满足
满足 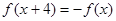 ,且
,且 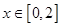 时,
时,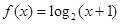 ,给出下列结论:
,给出下列结论:
①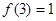 ; ②函数
; ②函数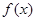 在
在 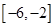 上是增函数;
上是增函数;
③函数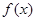 的图像关于直线x=1对称;
的图像关于直线x=1对称;
④若  ,则关于x的方程
,则关于x的方程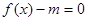 在[-8,16]上的所有根之和为12.
在[-8,16]上的所有根之和为12.
则其中正确的命题为_________.
推荐套卷
已知定义在R上的奇函数 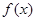 满足
满足 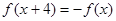 ,且
,且 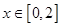 时,
时,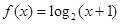 ,给出下列结论:
,给出下列结论:
①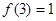 ; ②函数
; ②函数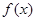 在
在 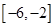 上是增函数;
上是增函数;
③函数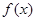 的图像关于直线x=1对称;
的图像关于直线x=1对称;
④若  ,则关于x的方程
,则关于x的方程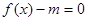 在[-8,16]上的所有根之和为12.
在[-8,16]上的所有根之和为12.
则其中正确的命题为_________.