设函数 .
.
(Ⅰ)当 时,讨论函数
时,讨论函数 的零点个数;
的零点个数;
(Ⅱ)若对于给定的实数 ,存在实数
,存在实数 ,使不等式
,使不等式 对于任意
对于任意 恒成立。试将最大实数
恒成立。试将最大实数 表示为关于
表示为关于 的函数
的函数 ,并求
,并求 的取值范围.
的取值范围.
(本小题满分14分)已知 为实数,对于实数
为实数,对于实数 和
和 ,定义运算“
,定义运算“ ”:
”: ,
,
设 .
.
(Ⅰ)若 在
在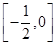 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)若方程 有三个不同的解,记此三个解的积为
有三个不同的解,记此三个解的积为 ,求
,求 的取值范围.
的取值范围.
已知函数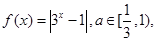 若函数
若函数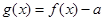 有两个不同的零点
有两个不同的零点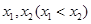 ,函数
,函数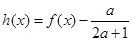 有两个不同的零点
有两个不同的零点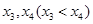 .
.
(1)若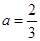 ,求
,求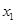 的值;
的值;
(2)求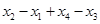 的最小值.
的最小值.
已知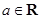 ,函数
,函数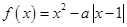 .
.
(Ⅰ)当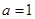 时,求函数
时,求函数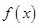 的最小值;
的最小值;
(Ⅱ)当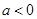 时,讨论
时,讨论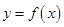 的图象与
的图象与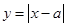 的图象的公共点个数.
的图象的公共点个数.
(本小题满分12分)
已知定义域为R的奇函数 满足
满足 ,且当
,且当 时,
时, .
.
(1)求 在区间[-1,1]上的解析式.
在区间[-1,1]上的解析式.
(2)当m取何值时,方程 在区间(0,1)上有解?
在区间(0,1)上有解?
(本小题满分12分)已知二次函数 对任意实数
对任意实数 都满足
都满足 ,且
,且 .令
.令 .
.
(1)若函数 在
在 上的最小值为0,求
上的最小值为0,求 的值;
的值;
(2)记函数 ,若函数
,若函数 有5个不同的零点,求实数
有5个不同的零点,求实数 的取值范围.
的取值范围.
定义在 上的函数
上的函数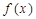 ,如果满足:对任意
,如果满足:对任意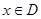 ,存在常数
,存在常数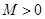 ,都有
,都有
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中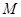 称为函数
称为函数 的上界.已知函数
的上界.已知函数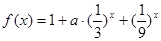 ,
,
(1)当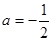 时,求函数
时,求函数 在
在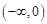 上的值域,并判断函数
上的值域,并判断函数 在
在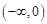 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数 在
在 上是以4为上界的有界函数,求实数
上是以4为上界的有界函数,求实数 的取值范围;
的取值范围;
(本小题满分14分)已知命题 :方程
:方程 有两个不相等的实根;命题
有两个不相等的实根;命题 :关于
:关于 的不等式
的不等式 对任意的实数
对任意的实数 恒成立.若“
恒成立.若“ ”为真,“
”为真,“ ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.