[江苏]2013-2014学年江苏苏州五市四区高一上学期期末调研测试数学卷
已知f(x)是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,若函数f(x)在区间[-1,t]上的最小值为-1,则实数t的取值范围是 .
,若函数f(x)在区间[-1,t]上的最小值为-1,则实数t的取值范围是 .
来源:2013-2014学年江苏苏州五市四区高一上学期期末调研测试数学卷
如图,过原点 的直线与函数
的直线与函数 的图象交于
的图象交于 两点,过
两点,过 作
作 轴的垂线交函数
轴的垂线交函数 的图象于点
的图象于点 ,若
,若 平行于
平行于 轴,则点
轴,则点 的坐标是 _ .
的坐标是 _ .
来源:2013-2014学年江苏苏州五市四区高一上学期期末调研测试数学卷
已知函数 的定义域为集合
的定义域为集合 .
.
(1)若函数 的定义域也为集合
的定义域也为集合 ,
, 的值域为
的值域为 ,求
,求 ;
;
(2)已知 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.
来源:2013-2014学年江苏苏州五市四区高一上学期期末调研测试数学卷
某厂生产某种产品 (百台),总成本为
(百台),总成本为 (万元),其中固定成本为2万元, 每生产1百台,成本增加1万元,销售收入
(万元),其中固定成本为2万元, 每生产1百台,成本增加1万元,销售收入 (万元),假定该产品产销平衡。
(万元),假定该产品产销平衡。
(1)若要该厂不亏本,产量 应控制在什么范围内?
应控制在什么范围内?
(2)该厂年产多少台时,可使利润最大?
(3)求该厂利润最大时产品的售价。
来源:2013-2014学年江苏苏州五市四区高一上学期期末调研测试数学卷
已知点 ,
, 是函数
是函数
 图象上的任意两点,且角
图象上的任意两点,且角 的终边经过点
的终边经过点 ,若
,若 时,
时, 的最小值为
的最小值为 .
.
(1)求函数 的解析式;
的解析式;
(2)求函数 的单调递增区间;
的单调递增区间;
(3)当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
来源:2013-2014学年江苏苏州五市四区高一上学期期末调研测试数学卷
 的最小正周期是 .
的最小正周期是 . 的定义域为___ _____.
的定义域为___ _____.  ,若
,若 与
与 平行,则实数
平行,则实数 = .
= . 的值域是__ ____.
的值域是__ ____.
 ,则
,则 __ ___.
__ ___. 的零点在区间
的零点在区间 内,则
内,则 .
. ,
, ,则
,则 _ ____.
_ ____. 在一个周期内的图象,则其解析式是___________.
在一个周期内的图象,则其解析式是___________.
 则
则 _ .
_ .
 ,则
,则 .
. 中, 底边
中, 底边 ,
,  ,
,  , 若
, 若 , 则
, 则 =___ __.
=___ __.
 ,函数
,函数 在区间
在区间 上的最大值等于
上的最大值等于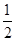 ,则
,则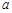 的值为 .
的值为 . .
. 的值;
的值; ,求
,求 的值;
的值; 中,
中, ,
, ,
, ,
, 。
。
 表示
表示 ;
; ,
, ,
, ,分别求
,分别求 和
和 的值。
的值。 .
. ,函数
,函数 在区间
在区间 上是单调递增函数,求实数
上是单调递增函数,求实数 的取值范围;
的取值范围; ,若对任意
,若对任意 恒成立,求
恒成立,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号