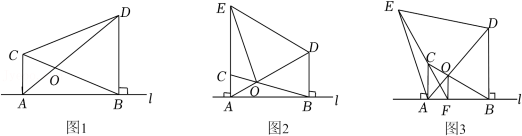
已知:点 均在直线 的上方, 与 都是直线 的垂线段,且 在 的右侧, , 与 相交于点 .
(1)如图1,若连接 ,则 的形状为 , 的值为 ;
(2)若将 沿直线 平移,并以 为一边在直线 的上方作等边 .
①如图2,当 与 重合时,连接 ,若 ,求 的长;
②如图3,当 时,连接 并延长交直线 于点 ,连接 .求证: .
如图,已知抛物线 经过 和 两点,直线 与 轴相交于点 , 是直线 上方的抛物线上的一个动点, 轴交 于点 .
(1)求该抛物线的表达式;
(2)若 轴交 于点 ,求 的最大值;
(3)若以 为顶点的三角形与 相似,请直接写出所有满足条件的点 ,点 的坐标.

如图,在 中, ,点 是 边的中点,点 在 边上, 经过点 且与 边相切于点 , .
(1)求证: 是 的切线;
(2)若 , ,求 的半径及 的长.

为了加强学生的体育锻炼,某班计划购买部分绳子和实心球.已知每条绳子的价格比每个实心球的价格少 元,且 元购买绳子的数量与 元购买实心球的数量相同.
(1)绳子和实心球的单价各是多少元?
(2)如果本次购买的总费用为 元,且购买绳子的数量是实心球数量的3倍,那么购买绳子和实心球的数量各是多少?
在贯彻落实“五育并举”的工作中,某校开设了五个社团活动:传统国学(A)、科技兴趣(B)、民族体育(C)、艺术鉴赏(D)、劳技实践(E),每个学生每个学期只参加一个社团活动.为了了解本学期学生参加社团活动的情况,学校随机抽取了若干名学生进行调查,并将调查结果绘制成如下两幅尚不完整的统计图.请根据统计图提供的信息,解答下列问题:
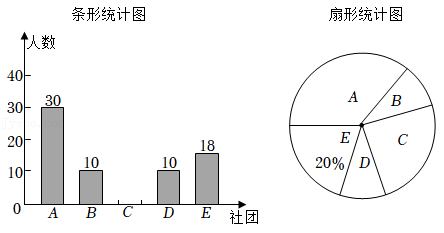
(1)本次调查的学生共有 人;
(2)将条形统计图补充完整;
(3)在扇形统计图中,传统国学(A)对应扇形的圆心角度数是 ;
(4)若该校有 名学生,请估算本学期参加艺术鉴赏(D)活动的学生人数.
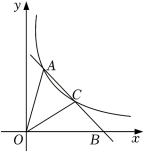
如图,直线 与反比例函数 的图象相交于点 和点 ,与 轴的正半轴相交于点 .
(1)求 的值;
(2)连接 ,若点 为线段 的中点,求 的面积.
综合与实践
“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.
提出问题:
如图1,在线段AC同侧有两点 ,连接 ,如果 ,那么 四点在同一个圆上.
探究展示:
如图2,作经过点 的 ,在劣弧 上取一点 (不与 重合),连接 ,则 (依据1)
∵
∴
∴点 四点在同一个圆上(对角互补的四边形四个顶点共圆)
∴点 在点 所确定的 上(依据2)
∴点 四点在同一个圆上
反思归纳:
(1)上述探究过程中的“依据1”、“依据2”分别是指什么?
依据1:__________;依据2:__________.
(2)如图3,在四边形 中, ,则 的度数为_____.
拓展探究:
(3)如图4,已知 是等腰三角形, ,点 在 上(不与 的中点重合),连接 .作点 关于 的对称点 ,连接 并延长交 的延长线于 ,连接 .
①求证: 四点共圆;
②若 , 的值是否会发生变化,若不变化,求出其值;若变化,请说明理由.


新定义:我们把抛物线 (其中 )与抛物线 称为“关联抛物线”.例如:抛物线 的“关联抛物线”为: .已知抛物线 的“关联抛物线”为 .
(1)写出 的解析式(用含 的式子表示)及顶点坐标;
(2)若 ,过 轴上一点 ,作 轴的垂线分别交抛物线 , 于点 .
①当 时,求点 的坐标;
②当 时, 的最大值与最小值的差为 ,求 的值.
遵义市开展信息技术与教学深度融合的“精准化教学”,某实验学校计划购买A,B两种型号教学设备,已知A型设备价格比B型设备价格每台高 ,用 元购买A型设备的数量比用 元购买B型设备的数量多 台.
(1)求A,B型设备单价分别是多少元;
(2)该校计划购买两种设备共 台,要求A型设备数量不少于B型设备数量的 .设购买a台A型设备,购买总费用为 元,求 与 的函数关系式,并求出最少购买费用.
如图1所示是一种太阳能路灯,它由灯杆和灯管支架两部分构成.如图2, 是灯杆, 是灯管支架,灯管支架 与灯杆间的夹角 .综合实践小组的同学想知道灯管支架 的长度,他们在地面的点 处测得灯管支架底部 的仰角为 ,在点 处测得灯管支架顶部 的仰角为 ,测得 ( 在同一条直线上).根据以上数据,解答下列问题:
(1)求灯管支架底部距地面高度 的长(结果保留根号);
(2)求灯管支架 的长度(结果精确到 ,参考数据: ).

将正方形 和菱形 按照如图所示摆放,顶点 与顶点 重合,菱形 的对角线 经过点 ,点 分别在 上.
(1)求证: ;
(2)若 ,求 的长.

如图所示,甲、乙两个带指针的转盘分别被分成三个面积相等的扇形(两个转盘除表面数字不同外,其它完全相同),转盘甲上的数字分别是 ,转盘乙上的数字分别是 (规定:指针恰好停留在分界线上,则重新转一次).
(1)转动转盘,转盘甲指针指向正数的概率是_____;转盘乙指针指向正数的概率是_____.
(2)若同时转动两个转盘,转盘甲指针所指的数字记为 ,转盘乙指针所指的数字记为 ,请用列表法或树状图法求满足 的概率.

在平面直角坐标系中,抛物线 (b是常数)经过点(2,0).点A在抛物线上,且点A的横坐标为m(m≠0).以点A为中心,构造正方形PQMN,PQ=2|m|,且PQ⊥x轴.
(1)求该抛物线对应的函数表达式;
(2)若点B是抛物线上一点,且在抛物线对称轴左侧.过点B作x轴的平行线交抛物线于另一点C,连结BC.当BC=4时,求点B的坐标;
(3)若m>0,当抛物线在正方形内部的点的纵坐标y随x的增大而增大时,或者y随x的增大而减小时,求m的取值范围;
(4)当抛物线与正方形PQMN的边只有2个交点,且交点的纵坐标之差为 时,直接写出m的值.