初中数学解答题

如图，在▱ABCD中， $AB＝4$， $AD＝BD=\sqrt{13}$，点M为边AB的中点．动点P从点A出发，沿折线 $AD﹣DB$以每秒 $\sqrt{13}$个单位长度的速度向终点B运动，连结PM．作点A关于直线PM的对称点 $A`$，连结 $A`P$、 $A`M$．设点P的运动时间为t秒，

（1）点D到边AB的距离为 　 　；

（2）用含t的代数式表示线段DP的长；

（3）连结 $A`D$，当线段 $A`D$最短时，求 $△DPA`$的面积；

（4）当 $M$、 $A`$、 $C$三点共线时，直接写出t的值．

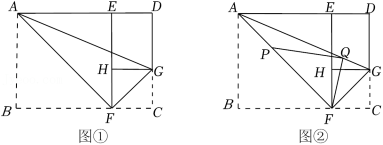
【探索发现】在一次折纸活动中，小亮同学选用了常见的A4纸，如图①，矩形ABCD为它的示意图．他查找了A4纸的相关资料，根据资料显示得出图①中 $AD=\sqrt{2}AB$．他先将A4纸沿过点A的直线折叠，使点B落在AD上，点B的对应点为点E，折痕为AF；再沿过点F的直线折叠，使点C落在EF上，点C的对应点为点H，折痕为FG；然后连结AG，沿AG所在的直线再次折叠，发现点D与点F重合，进而猜想 $△ADG≌△AFG$．

【问题解决】小亮对上面△ADG≌△AFG的猜想进行了证明，下面是部分证明过程：

证明：∵四边形ABCD是矩形，

∴ $\angle BAD＝\angle B＝\angle C＝\angle D＝90°$．

由折叠可知， $\angle BAF=\frac{1}{2}\angle BAD＝45°$， $\angle BFA＝\angle EFA$．

∴ $\angle EFA＝\angle BFA＝45°$．

∴ $AF=\sqrt{2}AB=AD$

请你补全余下的证明过程．

【结论应用】

（1）∠DAG的度数为 　 　度， $\frac{\mathit{FG}}{\mathit{AF}}$的值为 　 　；

（2）在图①的条件下，点P在线段AF上，且AP $=\frac{1}{2}$AB，点Q在线段AG上，连结FQ、PQ，如图②．设 $AB＝a$，则 $FQ+PQ$的最小值为 　 　．（用含a的代数式表示）

已知A、B两地之间有一条长440千米的高速公路．甲、乙两车分别从A、B两地同时出发，沿此公路相向而行，甲车先以100千米/时的速度匀速行驶200千米后与乙车相遇，再以另一速度继续匀速行驶4小时到达B地；乙车匀速行驶至A地，两车到达各自的目的地后停止，两车距A地的路程y（千米）与各自的行驶时间x（时）之间的函数关系如图所示．

（1）m＝　 　，n＝　 　；

（2）求两车相遇后，甲车距A地的路程y与x之间的函数关系式；

（3）当乙车到达A地时，求甲车距A地的路程．

党的十八大以来，我国把科技自立自强作为国家发展的战略支撑，科技事业发生了历史性、整体性、格局性变化，成功跨入创新型国家的行列，专利项目多项指数显著攀升．如图是长春市2016年到2020年专利授权情况的统计图．

根据以上信息回答下列问题：

（1）长春市从2016年到2020年，专利授权量最多的是 　 　年；

（2）长春市从2016年到2020年，专利授权量年增长率的中位数是 　 　；

（3）与2019年相比，2020年长春市专利授权量增加了 　 　件，专利授权量年增长率提高了 　 　个百分点；（注：1%为1个百分点）

（4）根据统计图提供的信息，有下列说法，正确的画“√”，错误的画“×”．

①因为2019年的专利授权量年增长率最低，所以2019年的专利授权量的增长量就最小． 　　

②与2018年相比，2019年的专利授权量年增长率虽然下降，但专利授权量仍然上升．这是因为专利授权量年增长率 $=\frac{\mathit{当年专利授权量}-\mathit{上一年专利授权量}}{\mathit{上一年专利授权量}}\times 100\%$，所以只要专利授权量年增长率大于零，当年专利授权量就一定增加． 　 　

③通过统计数据，可以看出长春市区域科技创新力呈上升趋势，为国家科技自立自强贡献吉林力量． 　 　

如图，在Rt△ABC中， $\angle ABC＝90°$， $AB＜BC$．点D是AC的中点，过点D作DE⊥AC交BC于点E．延长ED至点F，使得DF＝DE，连结AE、AF、CF．

（1）求证：四边形AECF是菱形；

（2）若 $\frac{\mathit{BE}}{\mathit{EC}}=\frac{1}{4}$，则 $\tan \angle BCF$的值为 　 　．

图①、图②、图③均是5×5的正方形网格，每个小正方形的边长均为1，其顶点称为格点，△ABC的顶点均在格点上．只用无刻度的直尺，在给定的网格中，按下列要求作图，保留作图痕迹．

（1）网格中△ABC的形状是 　 　；

（2）在图①中确定一点D，连结DB、DC，使△DBC与△ABC全等；

（3）在图②中△ABC的边BC上确定一点E，连结AE，使△ABE∽△CBA；

（4）在图③中△ABC的边AB上确定一点P，在边BC上确定一点Q，连结PQ，使△PBQ∽△ABC，且相似比为1：2．

为了让学生崇尚劳动，尊重劳动，在劳动中提升综合素质，某校定期开展劳动实践活动．甲、乙两班在一次体验挖土豆的活动中，甲班挖1500千克土豆与乙班挖1200千克土豆所用的时间相同．已知甲班平均每小时比乙班多挖100千克土豆，问乙班平均每小时挖多少千克土豆？

抛掷一枚质地均匀的普通硬币，仅有两种可能的结果：“出现正面”或“出现反面”，正面朝上记2分，反面朝上记1分．小明抛掷这枚硬币两次，用画树状图（或列表）的方法，求两次分数之和不大于3的概率．

现有若干张相同的半圆形纸片，点O是圆心，直径AB的长是12cm，C是半圆弧上的一点（点C与点A、B不重合），连接AC、BC．

（1）沿AC、BC剪下△ABC，则△ABC是 　 　三角形（填“锐角”、“直角”或“钝角”）；

（2）分别取半圆弧上的点E、F和直径AB上的点G、H．已知剪下的由这四个点顺次连接构成的四边形是一个边长为6cm的菱形．请用直尺和圆规在图中作出一个符合条件的菱形（保留作图痕迹，不要求写作法）；

（3）经过数次探索，小明猜想，对于半圆弧上的任意一点C，一定存在线段AC上的点M、线段BC上的点N和直径AB上的点P、Q，使得由这四个点顺次连接构成的四边形是一个边长为4cm的菱形．小明的猜想是否正确？请说明理由．

已知二次函数 $y＝a{x}^2+bx+3$的自变量x的部分取值和对应函数值y如下表：

x	…	﹣1	0	1	2	3	…
y	…	4	3	0	﹣5	﹣12	…

（1）求二次函数 $y＝a{x}^2+bx+3$的表达式；

（2）将二次函数 $y＝a{x}^2+bx+3$的图象向右平移k（k＞0）个单位，得到二次函数 $y＝m{x}^2+nx+q$的图象，使得当﹣1＜x＜3时，y随x增大而增大；当4＜x＜5时，y随x增大而减小．请写出一个符合条件的二次函数 $y＝m{x}^2+nx+q$的表达式y＝　 　，实数k的取值范围是 　 　；

（3）A、B、C是二次函数 $y＝a{x}^2+bx+3$的图象上互不重合的三点．已知点A、B的横坐标分别是m、m+1，点C与点A关于该函数图象的对称轴对称，求∠ACB的度数．

在四边形ABCD中，O是边BC上的一点．若 $△OAB≌△OCD$，则点O叫做该四边形的“等形点”．

（1）正方形 　 　“等形点”（填“存在”或“不存在”）；

（2）如图，在四边形ABCD中，边BC上的点O是四边形ABCD的“等形点”．已知 $CD＝4\sqrt{2}$， $OA＝5$， $BC＝12$，连接AC，求AC的长；

（3）在四边形EFGH中，EH∥FG．若边FG上的点O是四边形EFGH的“等形点”，求 $\frac{\mathit{OF}}{\mathit{OG}}$的值．

第十四届国际数学教育大会（ICME﹣14）会徽的主题图案有着丰富的数学元素，展现了我国古代数学的文化魅力，其右下方的“卦”是用我国古代的计数符号写出的八进制数3745．八进制是以8作为进位基数的数字系统，有0～7共8个基本数字．八进制数3745换算成十进制数是3×8³+7×8²+4×8¹+5×8⁰＝2021，表示ICME﹣14的举办年份．

（1）八进制数3746换算成十进制数是 　 　；

（2）小华设计了一个n进制数143，换算成十进制数是120，求n的值．

如图，点A在射线OX上，OA＝a．如果OA绕点O按逆时针方向旋转n°（0＜n≤360）到OA′，那么点A′的位置可以用（a，n°）表示．

（1）按上述表示方法，若a＝3，n＝37，则点A′的位置可以表示为 　 　；

（2）在（1）的条件下，已知点B的位置用（3，74°）表示，连接A′A、A′B．求证：A′A＝A′B．

如图，在平面直角坐标系xOy中，一次函数 $y＝2x+b$的图象分别与x轴、y轴交于点A、B，与反比例函数 $y=\frac{k}{x}$（x＞0）的图象交于点C，连接OC．已知点B（0，4），△BOC的面积是2．

（1）求b、k的值；

（2）求△AOC的面积．

在5张相同的小纸条上，分别写有语句：①函数表达式为y＝x；②函数表达式为y＝x²；③函数的图象关于原点对称；④函数的图象关于y轴对称；⑤函数值y随自变量x增大而增大．将这5张小纸条做成5支签，①、②放在不透明的盒子A中搅匀，③、④、⑤放在不透明的盒子B中搅匀．

（1）从盒子A中任意抽出1支签，抽到①的概率是 　 　；

（2）先从盒子A中任意抽出1支签，再从盒子B中任意抽出1支签．求抽到的2张小纸条上的语句对函数的描述相符合的概率．