如图,四边形 内接于 , 为 的直径, .
(1)试判断 的形状,并给出证明;
(2)若 , ,求 的长度.

为振兴乡村经济,在农产品网络销售中实行目标管理,根据目标完成的情况对销售员给予适当的奖励,某村委会统计了 名销售员在某月的销售额(单位:万元),数据如下:
(1)补全月销售额数据的条形统计图.

(2)月销售额在哪个值的人数最多(众数)?中间的月销售额(中位数)是多少?平均月销售额(平均数)是多少?
(3)根据(2)中的结果,确定一个较高的销售目标给予奖励,你认为月销额定为多少合适?
物理实验证实:在弹性限度内,某弹簧长度 与所挂物体质量 满足函数关系 .下表是测量物体质量时,该弹簧长度与所挂物体质量的数量关系.
|
|
|
|
|
|
|
|
(1)求 与 的函数关系式;
(2)当弹簧长度为 时,求所挂物体的质量.
《九章算术》是我国古代的数学专著,几名学生要凑钱购买 本.若每人出 元,则多了 元;若每人出 元,则少了 元.问学生人数和该书单价各是多少?
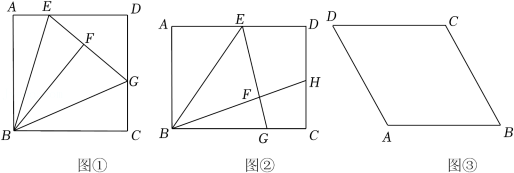
(1)发现:如图①所示,在正方形 中, 为AD边上一点,将 沿 翻折到 处,延长 交 边于 点.求证: ;
(2)探究:如图②,在矩形 中, 为 边上一点,且 .将 沿 翻折到 处,延长 交 边于 点,延长 交 边于点 ,且 ,求 的长.
(3)拓展:如图③,在菱形 中, , 为 边上的三等分点, .将 沿 翻折得到 ,直线 交 于点 ,求 的长.
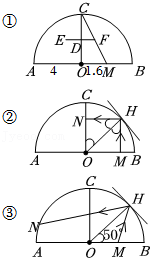
一个玻璃球体近似半圆 为直径.半圆 上点 处有个吊灯 , , 的中点为 , .
(1)如图①, 为一条拉线, 在 上, , ,求 的长度.
(2)如图②,一个玻璃镜与圆 相切, 为切点, 为 上一点, 为入射光线, 为反射光线, , ,求 的长度.
(3)如图③, 是线段 上的动点, 为入射光线, ,HN为反射光线交圆 于点N,在 从 运动到 的过程中,求 点的运动路径长.
二次函数 ,先向上平移 个单位,再向右平移 个单位,用光滑的曲线画在平面直角坐标系上.
|
|
|
|
|
|
|
|
|
|
|
|
(1) 的值为______;
(2)在坐标系中画出平移后的图象并写出 与 的交点坐标;
(3)点 在新的函数图象上,且 两点均在对称轴同一侧,若 ,则 ______ .(填不等号)

某学校打算购买甲乙两种不同类型的笔记本.已知甲种类型的笔记本的单价比乙种类型的要便宜 元,且用 购买的甲种类型的数量与用 元购买的乙种类型的数量一样.
(1)求甲乙两种类型笔记本的单价.
(2)该学校打算购买甲乙两种类型笔记本共 件,且购买的乙的数量不超过甲的 倍,则购买的最低费用是多少.
某工厂进行厂长选拔,从中抽出一部分人进行筛选,其中有“优秀”,“良好”,“合格”,“不合格”.

(1)本次抽查总人数为______,“合格”人数的百分比为______;
(2)补全条形统计图;
(3)扇形统计图中“不合格人数”的度数为______;
(4)在“优秀”中有甲乙丙三人,现从中抽出两人,则刚好抽中甲乙两人的概率为______.
综合与实践
【问题情境】
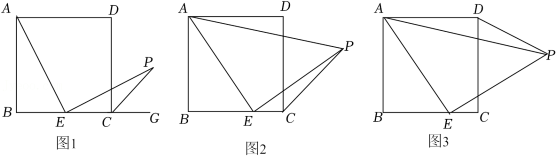
数学活动课上,老师出示了一个问题:如图1,在正方形 中,E是BC的中点, , 与正方形的外角 的平分线交于 点.试猜想 与 的数量关系,并加以证明;
【思考尝试】
(1)同学们发现,取 的中点 ,连接 可以解决这个问题.请在图1中补全图形,解答老师提出的问题.
【实践探究】
(2)希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形 中, 为 边上一动点(点 不重合), 是等腰直角三角形, ,连接 ,可以求出 的大小,请你思考并解答这个问题.
【拓展迁移】
(3)突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形 中, 为 边上一动点(点 不重合), 是等腰直角三角形, ,连接 .知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.