初中数学解答题

为减少传统塑料袋对生态环境的破坏，国家提倡使用可以在自然环境下（特定微生物、温度、湿度）较快完成降解的环保塑料袋．调查小组就某小区每户家庭1周内环保塑料袋的使用情况进行了抽样调查，使用情况为A（不使用）、B（1～3个）、C（4～6个）、D（7个及以上），以下是根据调查结果绘制的统计图的一部分．

（1）本次调查的样本容量是 　 　，请补全条形统计图；

（2）已知该小区有1500户家庭，调查小组估计：该小区1周内使用7个及以上环保塑料袋的家庭约有225户．调查小组的估计是否合理？请说明理由．

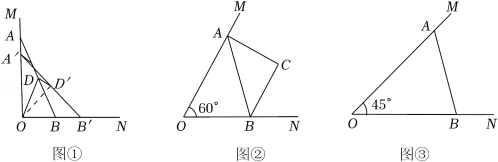
已知 $\angle MON＝\alpha$，点A，B分别在射线OM，ON上运动，AB＝6．

（1）如图①，若 $\alpha ＝90°$，取AB中点D，点A，B运动时，点D也随之运动，点A，B，D的对应点分别为A′，B′，D′，连接OD，OD′．判断OD与OD′有什么数量关系？证明你的结论；

（2）如图②，若 $\alpha ＝60°$，以AB为斜边在其右侧作等腰直角三角形ABC，求点O与点C的最大距离；

（3）如图③，若 $\alpha ＝45°$，当点A，B运动到什么位置时，△AOB的面积最大？请说明理由，并求出△AOB面积的最大值．

已知抛物线y＝﹣x²+2x+3与x轴交于A，B两点（点A在点B的左侧）．

（1）求点A，点B的坐标；

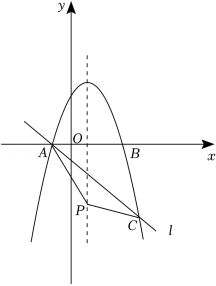
（2）如图，过点A的直线l：y＝﹣x﹣1与抛物线的另一个交点为C，点P为抛物线对称轴上的一点，连接PA，PC，设点P的纵坐标为m，当PA＝PC时，求m的值；

（3）将线段AB先向右平移1个单位长度，再向上平移5个单位长度，得到线段MN，若抛物线y＝a（﹣x²+2x+3）（a≠0）与线段MN只有一个交点，请直接写出a的取值范围．

如图，在 $△ABC$中， $AB＝AC$，以AC为直径作⊙O交BC于点D，过点D作 $DE\perp AB$，垂足为E，延长BA交⊙O于点F．

（1）求证：DE是⊙O的切线；

（2）若 $\frac{\mathit{AE}}{\mathit{DE}}=\frac{2}{3}$， $AF＝10$，求 $\odot O$的半径．

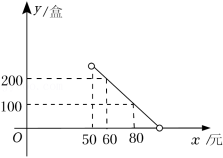
打油茶是广西少数民族特有的一种民俗．某特产公司近期销售一种盒装油茶，每盒的成本价为50元，经市场调研发现，该种油茶的月销售量y（盒）与销售单价x（元）之间的函数图象如图所示．

（1）求y与x的函数解析式，并写出自变量x的取值范围；

（2）当销售单价定为多少元时，该种油茶的月销售利润最大？求出最大利润．

综合与实践

【问题情境】数学活动课上，老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动．

【实践发现】同学们随机收集芒果树、荔枝树的树叶各10片，通过测量得到这些树叶的长y（单位：cm），宽x（单位：cm）的数据后，分别计算长宽比，整理数据如下：

	1	2	3	4	5	6	7	8	9	10
芒果树叶的长宽比	3.8	3.7	3.5	3.4	3.8	4.0	3.6	4.0	3.6	4.0
荔枝树叶的长宽比	2.0	2.0	2.0	2.4	1.8	1.9	1.8	2.0	1.3	1.9

【实践探究】分析数据如下：

	平均数	中位数	众数	方差
芒果树叶的长宽比	3.74	m	4.0	0.0424
荔枝树叶的长宽比	1.91	1.95	n	0.0669

【问题解决】

（1）上述表格中：m＝　 　，n＝　 　；

（2）①A同学说：“从树叶的长宽比的方差来看，我认为芒果树叶的形状差别大．”

②B同学说：“从树叶的长宽比的平均数、中位数和众数来看，我发现荔枝树叶的长约为宽的两倍．”

上面两位同学的说法中，合理的是 　　（填序号）；

（3）现有一片长11cm，宽5.6cm的树叶，请判断这片树叶更可能来自于芒果、荔枝中的哪种树？并给出你的理由．

如图，在 $▱ABCD$中，BD是它的一条对角线．

（1）求证： $△ABD≌△CDB$；

（2）尺规作图：作BD的垂直平分线EF，分别交AD，BC于点E，F（不写作法，保留作图痕迹）；

（3）连接BE，若 $\angle DBE＝25°$，求 $\angle AEB$的度数．

已知抛物线经过 $A（﹣1，0）、B（0，3）、C（3，0）$三点，O为坐标原点，抛物线交正方形 $OBDC$的边 $BD$于点 $E$，点 $M$为射线 $BD$上一动点，连接 $OM$，交 $BC$于点 $F$．

（1）求抛物线的表达式；

（2）求证： $\angle BOF＝\angle BDF$；

（3）是否存在点 $M$，使 $△MDF$为等腰三角形？若不存在，请说明理由；若存在，求 $ME$的长．

如图， $AB$为 $\odot O$的直径， $C$是 $\odot O$上一点，过点 $C$的直线交 $AB$的延长线于点 $M$，作 $AD\perp MC$，垂足为 $D$，已知 $AC$平分 $\angle MAD$．

（1）求证： $MC$是 $\odot O$的切线；

（2）若 $AB＝BM＝4$，求 $\tan \angle MAC$的值．

金鹰酒店有 $140$间客房需安装空调，承包给甲、乙两个工程队合作安装，每间客房都安装同一品牌同样规格的一台空调，已知甲工程队每天比乙工程队多安装 $5$台，甲工程队的安装任务有 $80$台，两队同时安装．问：

（1）甲、乙两个工程队每天各安装多少台空调，才能同时完成任务？

（2）金鹰酒店响应“绿色环保”要求，空调的最低温度设定不低于 $26℃$，每台空调每小时耗电 $1.5$度；据预估，每天至少有 $100$间客房有旅客住宿，旅客住宿时平均每天开空调约 $8$小时．若电费 $0.8$元/度，请你估计该酒店每天所有客房空调所用电费 $W$（单位：元）的范围？

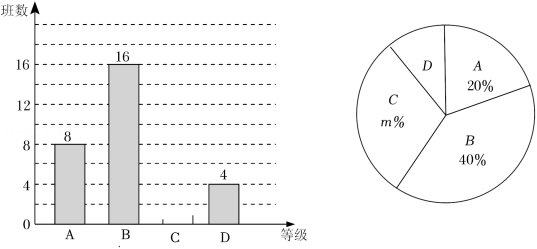
学校举行“爱我中华，朗诵经典”班级朗诵比赛，黄老师收集了所有参赛班级的成绩后，把成绩 $x$（满分 $100$分）分成四个等级（ $A：90\le x\le 100，B：80\le x＜90，C：70\le x＜80，D：60\le x＜70$）进行统计，并绘制成如下不完整的条形统计图和扇形统计图．

根据信息作答：

（1）参赛班级总数有＿＿＿＿＿个； $m＝$＿＿＿＿＿；

（2）补全条形统计图；

（3）统计发现D等级中七年级、八年级各有两个班，为了提高D等级班级的朗诵水平，语文组老师计划从D等级班级中任选两个班进行首轮培训，求选中两个班恰好是同一个年级的概率（用画树状图或列表法把所有可能结果表示出来）．

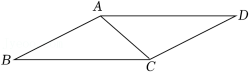
校园内有一块四边形的草坪造型，课外活动小组实地测量，并记录数据，根据造型画如图的四边形 $ABCD$，其中 $AB＝CD＝2$米， $AD＝BC＝3$米， $\angle B＝30°$．

（1）求证： $△ABC≌△CDA$；

（2）求草坪造型的面积．

已知：点 $A（1，3）$是反比例函数 $y_1=\frac{\mathrm{k}}{\mathrm{x}}（k\ne 0）$的图象与直线 $y_2＝mx（m\ne 0）$的一个交点．

（1）求 $k、m$的值；

（2）在第一象限内，当 $y_2＞y_1$时，请直接写出 $x$的取值范围．

解不等式 $2x+3\ge ﹣5$，并把解集在数轴上表示出来．

如图，抛物线 $y＝x^2+bx+c$（ $b，c$是常数）的顶点为 $C$，与 $x$轴交于 $A，B$两点， $A（1，0），AB＝4$，点 $P$为线段 $AB$上的动点，过 $P$作 $PQ\parallel BC$交 $AC$于点 $Q$．

（1）求该抛物线的解析式；

（2）求 $△CPQ$面积的最大值，并求此时 $P$点坐标．