已知函数 ,
, ,且
,且 在点
在点 处的切线方程为
处的切线方程为 .
.
(1)求 的解析式;
的解析式;
(2)求函数 的单调递增区间;
的单调递增区间;
(3)设函数 若方程
若方程 恰四个不同的解,求实数
恰四个不同的解,求实数 的取值范围.
的取值范围.
已知函数 ,
, 为常数.
为常数.
(1)若函数 在
在 处的切线与
处的切线与 轴平行,求
轴平行,求 的值;
的值;
(2)当 时,试比较
时,试比较 与
与 的大小;
的大小;
(3)若函数 有两个零点
有两个零点 、
、 ,试证明
,试证明 .
.
设函数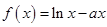 .
.
(1)当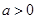 时,求函数
时,求函数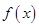 在区间
在区间 内的最大值;
内的最大值;
(2)当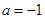 时,方程
时,方程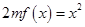 有唯一实数解,求正数
有唯一实数解,求正数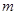 的值.
的值.
已知函数
(1)当a=2时,求函数y=f(x)的图象在x=0处的切线方程;
(2)判断函数f(x)的单调性;
(3)求证:
已知函数 的图象与直线
的图象与直线 交于点P,若图象在点P处的切线与x轴交点的横坐标为
交于点P,若图象在点P处的切线与x轴交点的横坐标为 ,则
,则 +
+ +…+
+…+ 的值为( )
的值为( )
| A.-1 | B.1-log20132012 | C.-log20132012 | D.1 |
已知函数f(x)=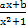 在点(-1,f(-1))处的切线方程为x+y+3=0.
在点(-1,f(-1))处的切线方程为x+y+3=0.
(1)求函数f(x)的解析式.
(2)设g(x)=lnx.求证:g(x)≥f(x)在[1,+∞)上恒成立.
如图,从点做
轴的垂线交曲线
于点
,曲线在
点处的切线与
轴交于点
,再从
做
轴的垂线交曲线于点
,依次重复上述过程得到一系列点:
,记
点的坐标为
.

(Ⅰ)试求与
的关系
;
(Ⅱ)求.
已知 的图像过原点,且在点
的图像过原点,且在点 处的切线与
处的切线与 轴平行,对任意
轴平行,对任意 ,都有
,都有 .
.
(1)求函数 在点
在点 处切线的斜率;
处切线的斜率;
(2)求 的解析式;
的解析式;
(3)设 ,对任意
,对任意 ,都有
,都有 .求实数
.求实数 的取值范围.
的取值范围.
【改编】已知函数 (
( ),若函数
),若函数 的图象在点
的图象在点 处的切线与直
处的切线与直
线 平行,则
平行,则 _______.
_______.