题客网高考押题卷 第四期(江苏版)数学
如图,圆周上按顺时针方向标有1,2,3,4,5五个点. 一只青蛙按顺时针方向绕圆从一个点跳到另一个点,若它停在奇数点上,则下次只能跳一个点;若停在偶数点上,则跳两个点. 该青蛙从“5”这点起跳,经2014次跳后它停在的点对应的数字是 .
在空间中,用 表示三条不同的直线,
表示三条不同的直线, 表示平面,给出下列四个命题:
表示平面,给出下列四个命题:
①若 ,
, ,则
,则 ; ②若
; ②若 ,
, ,则
,则 ;
;
③若 ,
, ,则
,则 ; ④若
; ④若 ,
, ,则
,则 ;
;
其中真命题的序号为 .
在平面直角坐标系中,点 是由不等式组
是由不等式组 所确定的平面区域内的动点,
所确定的平面区域内的动点, 是直线
是直线 上任意一点,
上任意一点, 为坐标原点,则
为坐标原点,则 的最小值为 .
的最小值为 .
(本小题满分14分) 在△ABC中,a,b,c分别为内角A,B,C的对边,且
(1)求A的大小;
(2)现给出三个条件:① ;②a=2;③
;②a=2;③ .请从中选择两个条件,使得确定的△ABC的面积最大.
.请从中选择两个条件,使得确定的△ABC的面积最大.
(本小题满分14分)如图,在正三棱柱ABC-A1B1C1中,D、E分别为CC1、A1B1的中点.
求证:C1E∥平面A1BD;
(2)求证:平面ABB1A1⊥平面A1BD.
(本小题满分14分)矩形纸片ABCD的边AB=6,AD=10,点E、F分别在边AB和BC上(不含端点). 现将纸片的右下角沿EF翻折,使得顶点B翻折后的新位置B1恰好落在边AD上. 设 ,EF=l,l关于t的函数为
,EF=l,l关于t的函数为 .
. 
试求:(1)函数f(t)的定义域;
(2)函数f(t)的最小值.
在平面直角坐标系 中,已知圆
中,已知圆 :
: ,圆
,圆 :
:
 (
( ,且
,且 ).
).
(1)设 为坐标轴上的点,满足:过点P分别作圆
为坐标轴上的点,满足:过点P分别作圆 与圆
与圆 的一条切线,切点分别为
的一条切线,切点分别为 、
、 ,使得
,使得 ,试求出所有满足条件的点
,试求出所有满足条件的点 的坐标;
的坐标;
(2)若斜率为正数的直线 平分圆
平分圆 ,求证:直线
,求证:直线 与圆
与圆 总相交.
总相交.
已知数列 的前
的前 项和
项和 满足:
满足: (t为常数,且
(t为常数,且 ).
).
(1)求 的通项公式;
的通项公式;
(2)设 ,试求t的值,使数列
,试求t的值,使数列 为等比数列;
为等比数列;
(3)在(2)的情形下,设 ,数列
,数列 的前
的前 项和为
项和为 ,若不等式
,若不等式 对
对
任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知函数 ,
, ,且
,且 在点
在点 处的切线方程为
处的切线方程为 .
.
(1)求 的解析式;
的解析式;
(2)求函数 的单调递增区间;
的单调递增区间;
(3)设函数 若方程
若方程 恰四个不同的解,求实数
恰四个不同的解,求实数 的取值范围.
的取值范围.
选修4—1几何证明选讲.
如图,在△ABC中,CM是∠ACB的平分线,△AMC的外接圆O交BC于点N. 若AB=2AC,求证:BN=2AM.
选修4—2:矩阵与变换
二阶矩阵M有特征值 ,其对应的一个特征向量e=
,其对应的一个特征向量e= ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点
变换成点 ,求矩阵M.
,求矩阵M.
选修4—4:坐标系与参数方程
在平面直角坐标系xOy中,以O为极点,Ox为极轴建立极坐标系,且两种坐标系长度单位一致. 已知直线l的极坐标方程为 ,圆C在直角坐标系中的参数方程为
,圆C在直角坐标系中的参数方程为 (
( 为参数),求直线l与圆C的公共点的个数.
为参数),求直线l与圆C的公共点的个数.
如图,正四棱锥 的底面边长为2a,高为h. 以其底面中心O为坐标原点建立空间直角坐标系
的底面边长为2a,高为h. 以其底面中心O为坐标原点建立空间直角坐标系 ,其中Ox//BC,Oy//AB,E为VC的中点.
,其中Ox//BC,Oy//AB,E为VC的中点.
(1)用a和h表示 ;
;
(2)当 是二面角
是二面角 的平面角时,求cos
的平面角时,求cos
 .
. . 在该矩形内任取一点P,则
. 在该矩形内任取一点P,则 的概率为 .
的概率为 . 有且仅有2个子集,则满足条件的实数
有且仅有2个子集,则满足条件的实数 的个数是 .
的个数是 .
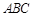 中,a,b,c分别是角A、B、C所对的边,若
中,a,b,c分别是角A、B、C所对的边,若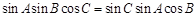
 ,若则
,若则 的最大值为 .
的最大值为 . 的单调递减区间是 .
的单调递减区间是 . ,且
,且 ,则
,则 的值为 .
的值为 . ,则
,则 的最大值是 .
的最大值是 . 是曲线
是曲线
 上不同的两点. 若直线
上不同的两点. 若直线 的斜率
的斜率 总满足
总满足 ,则实数
,则实数 的值是 .
的值是 . ,则函数
,则函数 的零点的个数为 .
的零点的个数为 . +
+ 的最小值是 .
的最小值是 . .
. 时,求函数
时,求函数 的定义域;
的定义域; 的定义域为R,试求
的定义域为R,试求 的取值范围.
的取值范围. 。求
。求
 及
及
 的关系式;
的关系式; 的通项公式
的通项公式

 粤公网安备 44130202000953号
粤公网安备 44130202000953号