福建省福州市高三上学期期末质量检测理科数学试卷
已知全集U=R,集合A={1,2,3,4,5},B=[3,十 ),则图中阴影部分所表示的集合为( )
),则图中阴影部分所表示的集合为( )
| A.{0,1,2} | B.{0,1}, | C.{1,2} | D.{1} |
设 是实数,若复数
是实数,若复数 (i为虚数单位)在复平面内对应的点在直线x+y=0上,则
(i为虚数单位)在复平面内对应的点在直线x+y=0上,则 的值为( )
的值为( )
| A.-1 | B.0 | C.1 | D.2 |
阅读程序框图,为使输出的数据为30,则判断框中应填人的条件为( )
| A.i≤4 | B.i≤5` | C.i≤6 | D.i≤7 |
将参加夏令营的500名学生编号为:001,002,…,500,采用系统抽样的方法抽取一个容量为50的样本,且随机抽得的号码为003,这500名学生分住在三个营区,从001到200在第一营区,从201到355在第二营区,从356到500在第三营区,三个营区被抽中的人数为( )
| A.20,15,15 | B.20,16,14 | C.12,14,16 | D.21,15,14 |
已知函数 的图像在点A(l,f(1))处的切线l与直线x十3y+2=0垂直,若数列
的图像在点A(l,f(1))处的切线l与直线x十3y+2=0垂直,若数列 的前n项和为
的前n项和为 ,则S2013的值为 ( )
,则S2013的值为 ( )
A. |
B. |
C. |
D. |
如图,△ABC中,∠C =90°,且AC=BC=4,点M满足 ,则
,则 =( )
=( )
| A.2 | B.3 | C.4 | D.6 |
如图,偶函数f(x)的图像形如字母M,奇函数g(x)的图像形如字母N,若方程 的实根个数分别为a,b,c,d,则a+b+c+d=( )
的实根个数分别为a,b,c,d,则a+b+c+d=( )
| A.27 | B.30 | C.33 | D.36 |
已知函数f(x十1)是定义在R上的奇函数,若对于任意给定的不等实数 ,不等式
,不等式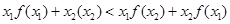 恒成立,则不等式f(1-x)<0的解集为( )
恒成立,则不等式f(1-x)<0的解集为( )
A.(1,+ ) ) |
B.(一 ,0) ,0) |
C.(0,+ ) ) |
D.(一 ,1) ,1) |
在平面直角坐标系xoy中,过坐标原点的一条直线与函数 的图像交于P、Q两点,则线段PQ长的最小值是____
的图像交于P、Q两点,则线段PQ长的最小值是____
如图,三角形数阵满足:
(1)第n行首尾两数均为n;
(2)表中的递推关系类似杨辉三角4则第n行(n≥2)第2个数是____.
给出下列命题:
①“x=一1”是“x2一5x一6=0”的必要不充分条件;
②在△ABC中,已知 则
则 ;
;
③在边长为1的正方形ABCD内随机取一点M,MA<1的概率为于
④若命题p是::对任意的 ,都有sinx≤1,则
,都有sinx≤1,则 为:存在
为:存在 ,使得sinx > 1.
,使得sinx > 1.
其中所有真命题的序号是____
为了倡导健康、低碳、绿色的生活理念,某市建立了公共自行车服务系统鼓励市民租用公共自行车出行,公共自行车按每车每次的租用时间进行收费,具体收费标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,收费1元;
③租用时间为2小时以上且不超过3小时,收费2元;
④租用时间超过3小时的时段,按每小时2元收费(不足1小时的部分按1小时计算)
已知甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0.4和0.5;租用时间为1小时以上且不超过2小时的概率分别是0.5和0.3.
(1)求甲、乙两人所付租车费相同的概率;
(2)设甲、乙两人所付租车费之和为随机变量 ,求
,求 的分布列和数学期望E
的分布列和数学期望E .
.
某工厂的固定成本为3万元,该工厂每生产100台某产品的生产成本为1万元,设生产该产品x(百台),其总成本为g(x)万元(总成本=固定成本+生产成本),并且销售收人r(x)满足 假定该产品产销平衡,根据上述统计规律求:
假定该产品产销平衡,根据上述统计规律求:
(1)要使工厂有盈利,产品数量x应控制在什么范围?
(2)工厂生产多少台产品时盈利最大?
已知中心在原点的双曲线C的一个焦点是F1(一3,0),一条渐近线的方程是
(1)求双曲线C的方程;
(2)若以k(k≠0)为斜率的直线 与双曲线C相交于两个不同的点M, N,且线段MN的
与双曲线C相交于两个不同的点M, N,且线段MN的
垂直平分线与两坐标轴围成的三角形的面积为 ,求k的取值范围。
,求k的取值范围。
 则a,b,c的大小关系为
则a,b,c的大小关系为 的展开式中,二次项系数最大的项是( )
的展开式中,二次项系数最大的项是( ) ,则函数
,则函数 的图象的一条对称轴方程为( )
的图象的一条对称轴方程为( )



 的离心率为( )
的离心率为( )

 或
或 所表示的平面区域的面积是9,则实数a的值为____.
所表示的平面区域的面积是9,则实数a的值为____.
 ,函数
,函数
 中,
中,
 是等比数列,并求
是等比数列,并求


 粤公网安备 44130202000953号
粤公网安备 44130202000953号