已知函数 在
在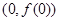 处切线为
处切线为 .
.
(1)求 的解析式;
的解析式;
(2)设 ,
, ,
, ,
, 表示直线
表示直线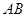 的斜率,求证:
的斜率,求证: .
.
已知函数 ,
,
(1)若 有最值,求实数
有最值,求实数 的取值范围;
的取值范围;
(2)当 时,若存在
时,若存在 ,使得曲线
,使得曲线 在
在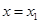 与
与 处的切线互相平行,求证
处的切线互相平行,求证 。
。
设函数 的定义域是
的定义域是 ,其中常数
,其中常数 .
.
(1)若 ,求
,求 的过原点的切线方程.
的过原点的切线方程.
(2)当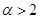 时,求最大实数
时,求最大实数 ,使不等式
,使不等式 对
对 恒成立.
恒成立.
(3)证明当 时,对任何
时,对任何 ,有
,有 .
.
已知函数 (
( ,
, 为自然对数的底数).
为自然对数的底数).
(1)若曲线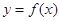 在点
在点 处的切线平行于
处的切线平行于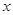 轴,求
轴,求 的值;
的值;
(2)求函数 的极值;
的极值;
(3)当 的值时,若直线
的值时,若直线 与曲线
与曲线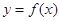 没有公共点,求
没有公共点,求 的最大值.
的最大值.
(注:可能会用到的导数公式: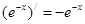 ;
; )
)
已知函数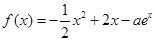 。
。
(1)若 ,求
,求 在
在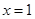 处的切线方程;
处的切线方程;
(2)若 在R上是增函数,求实数
在R上是增函数,求实数 的取值范围。
的取值范围。
(本小题满分15分)已知函数
(Ⅰ)若曲线 在点
在点 处的切线与直线
处的切线与直线 平行,求
平行,求 的值;
的值;
(Ⅱ)记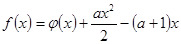 ,
, ,且
,且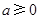 .求函数
.求函数 的单调递增区间.
的单调递增区间.
已知函数 .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)当 时,讨论
时,讨论 的单调性.
的单调性.
已知函数 .
.
(Ⅰ)当 时,求函数
时,求函数 在
在 处的切线方程;
处的切线方程;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)若函数 有两个极值点
有两个极值点 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知函数 处取得极值2
处取得极值2
(1)求函数 的表达式;
的表达式;
(2)当 满足什么条件时,函数
满足什么条件时,函数 在区间
在区间 上单调递增?
上单调递增?
(3)若 为
为 图象上任意一点,直线与
图象上任意一点,直线与 的图象相切于点P,求直线的斜率
的图象相切于点P,求直线的斜率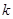 的取值范围
的取值范围
已知函数 图像上一点
图像上一点 处的切线方程为
处的切线方程为 (1)求
(1)求 的值;(2)若方程
的值;(2)若方程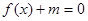 在区间
在区间 内有两个不等实根,求
内有两个不等实根,求 的取值范围;(3)令
的取值范围;(3)令 如果
如果 的图像与
的图像与 轴交于
轴交于 两点,
两点,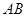 的中点为
的中点为 ,求证:
,求证: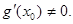
若曲线f(x,y)=0上两个不同点处的切线重合,则称这条切线为曲线f(x,y)=0的“自公切线”.下列方程:①x2-y2=1;②y=x2-|x|;③y=3sin x+4cos x;④|x|+1=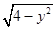 对应的曲线中存在“自公切线”的有 ()
对应的曲线中存在“自公切线”的有 ()
| A.①② | B.②③ | C.①④ | D.③④ |
已知函数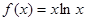 ,
,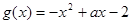 (
( ,
, ).
).
(1)判断曲线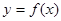 在点(1,
在点(1, )处的切线与曲线
)处的切线与曲线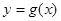 的公共点个数;
的公共点个数;
(2)当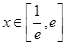 时,若函数
时,若函数 有两个零点,求
有两个零点,求 的取值范围.
的取值范围.
已知函数 (
( )
)
(1)若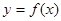 在点
在点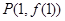 处的切线方程为
处的切线方程为 ,求
,求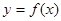 的解析式及单调递减区间;
的解析式及单调递减区间;
(2)若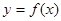 在
在 上存在极值点,求实数
上存在极值点,求实数 的取值范围.
的取值范围.
已知函数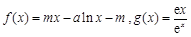 ,其中m,a均为实数.
,其中m,a均为实数.
(1)求 的极值;
的极值;
(2)设 ,若对任意的
,若对任意的
 ,
, 恒成立,求
恒成立,求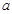 的最小值;
的最小值;
(3)设 ,若对任意给定的
,若对任意给定的 ,在区间
,在区间 上总存在
上总存在 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.