高考数学全程总复习课时提升作业四十 第六章第六节练习卷
在证明命题“对于任意角θ,cos4θ-sin4θ=cos2θ”的过程:“cos4θ-sin4θ=(cos2θ+sin2θ)·(cos2θ-sin2θ)=cos2θ-sin2θ=cos2θ”中应用了( )
| A.分析法 |
| B.综合法 |
| C.分析法和综合法综合使用 |
| D.间接证法 |
要证明a2+b2-1-a2b2≤0,只要证明( )
| A.2ab-1-a2b2≤0 | B.a2+b2-1-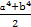 ≤0 ≤0 |
C. -1-a2b2≤0 -1-a2b2≤0 |
D.(a2-1)(b2-1)≥0 |
如果a<0,b<0,则必有( )
| A.a3+b3≥ab2+a2b | B.a3+b3≤ab2+a2b |
| C.a3+b3>ab2+a2b | D.a3+b3<ab2+a2b |
若实数a,b满足a+b<0,则( )
| A.a,b都小于0 |
| B.a,b都大于0 |
| C.a,b中至少有一个大于0 |
| D.a,b中至少有一个小于0 |
若P= +
+ ,Q=
,Q= +
+ (a≥0),则P,Q的大小关系是( )
(a≥0),则P,Q的大小关系是( )
| A.P>Q | B.P=Q |
| C.P<Q | D.由a的取值确定 |
若|loga |=loga
|=loga ,|logba|=-logba,则a,b满足的条件是( )
,|logba|=-logba,则a,b满足的条件是( )
| A.a>1,b>1 | B.0<a<1,b>1 |
| C.a>1,0<b<1 | D.0<a<1,0<b<1 |
已知函数f(x)是R上的单调增函数且为奇函数,数列{an}是等差数列,a3>0,则f(a1)+f(a3)+f(a5)的值( )
| A.恒为正数 | B.恒为负数 |
| C.恒为0 | D.可正可负 |
已知函数f(x)是定义在R上不恒为零的函数,且对于任意实数a,b∈R,满足:f(a·b)=af(b)+bf(a),f(2)=2,an= (n∈N*),bn=
(n∈N*),bn= (n∈N*).
(n∈N*).
考察下列结论:
①f(0)=f(1);②f(x)为偶函数;
③数列{an}为等比数列;
④数列{bn}为等差数列.
其中正确的结论共有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知f(1,1)=1,f(m,n)∈N*(m,n∈N*),且对任意的m,n∈N*都有:
(1)f(m,n+1)=f(m,n)+2.
(2)f(m+1,1)=2f(m,1).
给出以下三个结论:①f(1,5)=9;②f(5,1)=16;
③f(5,6)=26.其中正确结论的序号有 .
已知实数a,b,c,d满足a+b=c+d=1,ac+bd>1,求证:a,b,c,d中至少有一个是负数.
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.
(1)sin213°+cos217°-sin 13°cos 17°.
(2)sin215°+cos215°-sin 15°cos 15°.
(3)sin218°+cos212°-sin 18°cos 12°.
(4)sin2(-18°)+cos248°-sin(-18°)cos 48°.
(5)sin2(-25°)+cos255°-sin(-25°)cos 55°.
①试从上述五个式子中选择一个,求出这个常数.
②根据①的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
 +b
+b >a
>a ,Q=
,Q= -
- ,R=
,R= -
-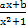 在点(-1,f(-1))处的切线方程为x+y+3=0.
在点(-1,f(-1))处的切线方程为x+y+3=0. 粤公网安备 44130202000953号
粤公网安备 44130202000953号