湖南省怀化市高三第二次模拟考试文科数学试卷
下列有关命题的说法中错误的是
A.若“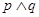 ”为真命题,则 ”为真命题,则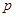 、 、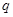 均为真命题 均为真命题 |
B.若命题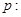 “ “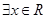 , ,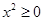 ”则命题 ”则命题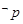 为“ 为“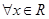 , ,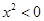 ” ” |
C.“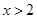 ”是“ ”是“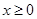 ”的充分不必要条件 ”的充分不必要条件 |
D.“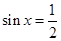 ”的必要不充分条件是“ ”的必要不充分条件是“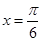 ” ” |
将函数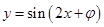 的图象沿
的图象沿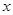 轴向左平移
轴向左平移 个单位后,得到一个关于
个单位后,得到一个关于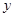 轴对称的图象,则
轴对称的图象,则
的一个可能取值为( )
A. |
B. |
C.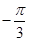 |
D.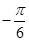 |
已知双曲线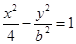 的右焦点与抛物线
的右焦点与抛物线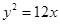 的焦点重合,则该双曲线的焦点到其渐近线的距离为( )
的焦点重合,则该双曲线的焦点到其渐近线的距离为( )
A.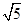 |
B.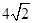 |
C.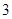 |
D.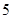 |
设定义域为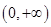 的单调函数
的单调函数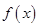 ,对任意的
,对任意的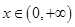 ,都有
,都有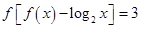 ,若
,若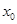 是方程
是方程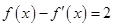 的一个解,则
的一个解,则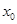 可能存在的区间是( )
可能存在的区间是( )
A.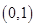 |
B.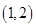 |
C.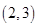 |
D.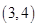 |
在平面直角坐标系 中,已知曲线
中,已知曲线 (
( 为参数),将曲线
为参数),将曲线 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的 、
、 倍后得到曲线
倍后得到曲线 的直角坐标方程为 .
的直角坐标方程为 .
某广告公司设计一个凸八边形的商标,它的中间是一个正方形,外面是四个腰长为 ,顶角为
,顶角为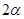 的等腰三角形.
的等腰三角形.
(1)若角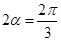 时,求该八边形的面积;
时,求该八边形的面积;
(2)写出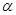 的取值范围,当
的取值范围,当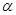 取何值时该八边形的面积最大,并求出最大面积.
取何值时该八边形的面积最大,并求出最大面积.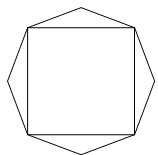
2013年11月,青岛发生输油管道爆炸事故造成胶州湾局部污染.国家海洋局用分层抽样的方法从国家环保专家、海洋生物专家、油气专家三类专家库中抽取若干人组成研究小组赴泄油海域工作,有关数据见表1(单位:人)
海洋生物专家为了检测该地受污染后对海洋动物身体健康的影响,随机选取了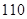 只海豚进行了检测,并将有关数据整理为不完整的
只海豚进行了检测,并将有关数据整理为不完整的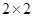 列联表,如表2.
列联表,如表2.
(1)求研究小组的总人数;
(2)写出表2中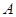 、
、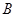 、
、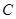 、
、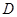 、
、 的值,并判断有多大的把握认为海豚身体不健康与受到污染有关;
的值,并判断有多大的把握认为海豚身体不健康与受到污染有关;
(3)若从研究小组的环保专家和海洋生物专家中随机选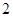 人撰写研究报告,求其中恰好有
人撰写研究报告,求其中恰好有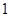 人为环保专家的概率.
人为环保专家的概率.
附:①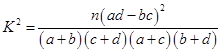 ,其中
,其中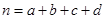 .
.
②
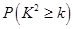 |
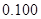 |
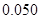 |
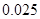 |
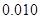 |
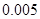 |
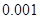 |
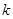 |
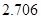 |
 |
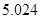 |
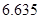 |
 |
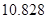 |
如图,在直三棱柱 中,
中, ,
, ,且异面直线
,且异面直线 与
与 所成的角等于
所成的角等于 .
.
(1)求棱柱的高;
(2)求 与平面
与平面 所成的角的大小.
所成的角的大小.
已知数列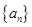 满足
满足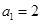 ,向量
,向量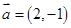 ,
,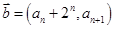 且
且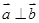 .
.
(1)求证数列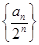 为等差数列,并求
为等差数列,并求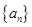 通项公式;
通项公式;
(2)设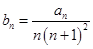 ,若对任意
,若对任意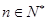 都有
都有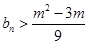 成立,求实数
成立,求实数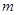 的取值范围.
的取值范围.
如图,椭圆 的长轴长为
的长轴长为 ,点
,点 、
、 、
、 为椭圆上的三个点,
为椭圆上的三个点, 为椭圆的右端点,
为椭圆的右端点, 过中心
过中心 ,且
,且 ,
, .
.
(1)求椭圆的标准方程;
(2)设 、
、 是椭圆上位于直线
是椭圆上位于直线 同侧的两个动点(异于
同侧的两个动点(异于 、
、 ),且满足
),且满足 ,试讨论直线
,试讨论直线 与直线
与直线 斜率之间的关系,并求证直线
斜率之间的关系,并求证直线 的斜率为定值.
的斜率为定值.
 的模为( )
的模为( )



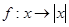 是集合
是集合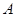 到集合
到集合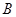 的映射,若
的映射,若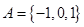 ,则
,则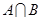 为( )
为( )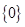
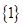
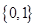
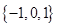
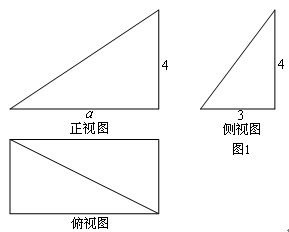
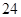 ,则正视图中
,则正视图中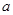 的值为( )
的值为( )
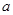 、
、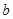 都是正实数,函数
都是正实数,函数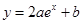 的图象过
的图象过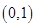 点,则
点,则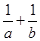 的最小值是( )
的最小值是( )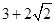
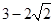
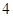
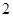
 ,
, ,且
,且 ,则
,则 与
与 的夹角是( )
的夹角是( )




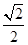
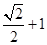
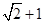
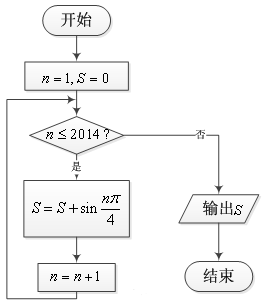
 的公比
的公比 ,其前
,其前 项和
项和 ,则
,则 .
. 、
、 、
、 的三角形区域内随机爬行,则其到三角形顶点的距离小于
的三角形区域内随机爬行,则其到三角形顶点的距离小于 的地方的概率为 .
的地方的概率为 . 、
、 满足约束条件
满足约束条件 ,则
,则 的最小值是 .
的最小值是 . ,
, 且
且 ,
, 时,
时, ; 当
; 当 .
.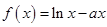 .
.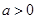 时,求函数
时,求函数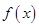 在区间
在区间 内的最大值;
内的最大值;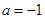 时,方程
时,方程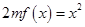 有唯一实数解,求正数
有唯一实数解,求正数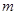 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号