高中数学组合几何试题

设函数，，，
（1）若曲线与轴相切于异于原点的一点，且函数的极小值为，求的值；
（2）若，且，
①求证：； ②求证：在上存在极值点．

已知函数f（x）=k（x﹣1）e^x+x²．
（Ⅰ）当时k=﹣，求函数f（x）在点（1，1）处的切线方程；
（Ⅱ）若在y轴的左侧，函数g（x）=x²+（k+2）^x的图象恒在f（x）的导函数f′（x）图象的上方，求k的取值范围；
（Ⅲ）当k≤﹣l时，求函数f（x）在[k，1]上的最小值m．

已知函数与轴相切若直线与分别交的图象于四点且四边形的面积为25则正实数的值为  

已知函数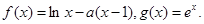
（1）求函数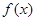的单调区间；
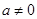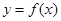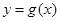（2）当时，过原点分别作曲线和的切线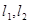，已知两切线的斜率互为倒数，证明：；
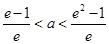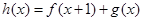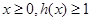（3）设，当时，求实数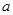的取值范围．

我们把形如的函数称为幂指函数，幂指函数在求导时，可以利用对数法：在函数解析式两边取对数得，两边对x求导数，得于是，
运用此方法可以求得函数在（1，1）处的切线方程是         .

已知函数，在点处的切线方程为．
（Ⅰ）求的解析式；
（Ⅱ）求的单调区间；
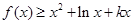（Ⅲ）若在区间内，恒有成立，求的取值范围．

已知函数与函数在点处有公共的切线，设.
（1） 求的值
（2）求在区间上的最小值.

（本小题满分13分）
函数，数列和满足：，，函数的图像在点处的切线在轴上的截距为.
（1）求数列{}的通项公式；
（2）若数列的项中仅最小,求的取值范围；
（3）若函数，令函数数列满足:且证明:.

设，．
（1）当时，求曲线在处的切线方程；
（2）如果存在，使得成立，求满足上述条件的最大整数；
（3）如果对任意的，都有成立，求实数的取值范围

已知函数
(1)若，求曲线在处的切线方程；
(2)求的单调区间；
(3）设，若对任意，均存在，使得，求的取值范围.

已知函数.
（1）当时，讨论函数的单调性；
（2）当时，在函数图象上取不同两点A、B，设线段AB的中点为，试探究函数在Q点处的切线与直线AB的位置关系？
（3）试判断当时图象是否存在不同的两点A、B具有（2）问中所得出的结论.

已知函数（k为常数，e=2.71828…是自然对数的底数），曲线在点处的切线与x轴平行．
(1)求k的值及的单调区间;
(2)设其中为的导函数,证明:对任意,.

已知函数f（x）＝x（x＋a）－lnx，其中a为常数.
（1）求f（x）的单调区间；
（2）问过坐标原点可以作几条直线与曲线y＝f（x）相切？并说明理由；
（3）若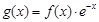在区间（0，1）内是单调函数，求a的取值范围.

设，其中为常数．
（1）求曲线（x）在点（4，2）处的切线方程；
（2）如果函数（x）的图象也经过点（4，2），求（x）与（1）中的切线的交点．

已知函数的图像为曲线C，若曲线C存在与直线垂直的切线则实数m的取值范围是 （    ）

A．

B．

C．

D．