已知函数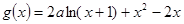
.
（1）当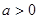
时，讨论函数
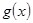的单调性；
（2）当
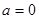时，在函数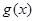
图象上取不同两点A、B，设线段AB的中点为
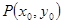，试探究函数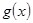在Q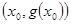
点处的切线与直线AB的位置关系？
（3）试判断当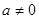
时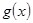图象是否存在不同的两点A、B具有（2）问中所得出的结论.
的图象的一部分，求这个函数的解析式．
是锐角，且
，求
的最小值．
，
，试判断
，
所在象限．
皆为锐角，且
，求
的值．
；
．相关知识点
推荐套卷
已知函数.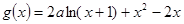
（1）当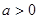时，讨论函数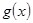的单调性；
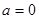（2）当时，在函数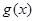图象上取不同两点A、B，设线段AB的中点为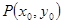，试探究函数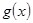在Q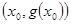点处的切线与直线AB的位置关系？
（3）试判断当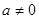时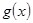图象是否存在不同的两点A、B具有（2）问中所得出的结论.
粤公网安备 44130202000953号