已知函数f(x)=k(x﹣1)ex+x2.
(Ⅰ)当时k=﹣ ,求函数f(x)在点(1,1)处的切线方程;
,求函数f(x)在点(1,1)处的切线方程;
(Ⅱ)若在y轴的左侧,函数g(x)=x2+(k+2)x的图象恒在f(x)的导函数f′(x)图象的上方,求k的取值范围;
(Ⅲ)当k≤﹣l时,求函数f(x)在[k,1]上的最小值m.
已知对任意的实数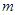 ,直线
,直线 都不与曲线
都不与曲线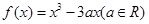 相切.
相切.
(1)求实数 的取值范围;
的取值范围;
(2)当 时,函数
时,函数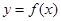 的图象上是否存在一点
的图象上是否存在一点 ,使得点
,使得点 到
到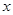 轴的距离不小于
轴的距离不小于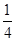 .试证明你的结论.
.试证明你的结论.
已知函数 R).
R).
(1)若曲线 在点
在点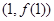 处的切线与直线
处的切线与直线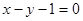 平行,求
平行,求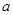 的值;
的值;
(2)在(1)条件下,求函数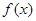 的单调区间和极值;
的单调区间和极值;
(3)当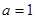 ,且
,且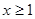 时,证明:
时,证明: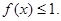
已知函数f(x)=x2﹣(a+2)x+alnx(a为实常数).
(Ⅰ)若a=﹣2,求曲线 y=f(x)在x=1处的切线方程;
(Ⅱ)讨论函数f(x)在[1,e]上的单调性;
(Ⅲ)若存在x∈[1,e],使得f(x)≤0成立,求实数a的取值范围.
设f(x)=a(x﹣5)2+6lnx,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
(1)确定a的值;
(2)求函数f(x)的单调区间与极值.
已知函数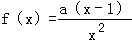 ,其中a>0.
,其中a>0.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若直线x﹣y﹣1=0是曲线y=f(x)的切线,求实数a的值;
(Ⅲ)设g(x)=xlnx﹣x2f(x),求g(x)在区间[1,e]上的最小值.(其中e为自然对数的底数)
已知函数f(x)=x2+2bx的图象在点A(0,f(0))处的切线l与直线x+y+3=0垂直,若数列{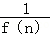 }的前n项和为Sn,则S2011的值为()
}的前n项和为Sn,则S2011的值为()
A.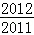 |
B.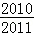 |
C.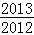 |
D.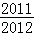 |