高中数学组合几何试题

（本小题满分12分）已知函数（其中是实数）．
（Ⅰ）求的单调区间；
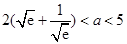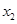（Ⅱ）若设，且有两个极值点，（），求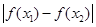的取值范围．（其中为自然对数的底数，）．

        ．

（本小题满分12分）已知函数f（x）＝x²－2（a＋1）x＋2alnx（a>0）．
（1）当a＝1时，求曲线y＝f（x）在点（1，f（1））处的切线方程；
（2）求f（x）的单调区间；
（3）若f（x）≤0在区间[1，e]上恒成立，求实数a的取值范围．

函数在其极值点处的切线方程为____________．

一质点运动时速度与时间的关系为v（t）＝t²－t＋2，质点做直线运动，则此物体在时间[1,2]内的位移为（ ）

A．

B．

C．

D．

函数在区间上的平均变化率为        ．

设函数，则下列结论正确的是（   ）

A．函数上单调递增

B．函数上单调递减

C．若，则函数的图象在点处的切线方程为y=10

D．若b=0，则函数的图象与直线y=10只有一个公共点

设曲线y＝在点（3，2）处的切线与直线ax＋y＋3＝0垂直，则a等于  （   ）

A．2

B．－2

C．

D．－

函数的图像在处的切线方程是                 ．

若曲线在处的切线与直线垂直，则

A．

B．

C．

D．

曲线与曲线公切线（切线相同）的条数为              ．

若，则       ．

若点是曲线上任意一点，则点到直线的最小距离为（  ）

A．

B．

C．

D．

（本小题满分12分）已知函数（为自然对数的底数），曲线在点处的切线方程为．
（1）求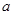，的值；
（2）任意，时，证明：．

（本小题满分12分）已知函数（为自然对数的底数），曲线在点处的切线方程为．
（1）求，的值；
（2）任意，时，证明：．