已知函数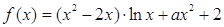 .
.
(1)当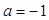 时,求
时,求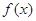 在
在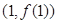 处的切线方程;
处的切线方程;
(2)设函数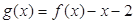 ,
,
(ⅰ)若函数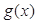 有且仅有一个零点时,求
有且仅有一个零点时,求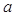 的值;
的值;
(ⅱ)在(ⅰ)的条件下,若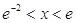 ,
, ,求
,求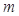 的取值范围。
的取值范围。
已知命题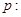
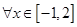 ,函数
,函数 的值大于
的值大于 .若
.若 是真命题,则命题
是真命题,则命题 可以是( )
可以是( )
A.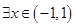 ,使得 ,使得 |
B.“ ”是“函数 ”是“函数 在区间 在区间 上有零点”的必要不充分条件 上有零点”的必要不充分条件 |
C.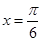 是曲线 是曲线 的一条对称轴 的一条对称轴 |
D.若 ,则在曲线 ,则在曲线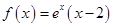 上任意一点处的切线的斜率不小于 上任意一点处的切线的斜率不小于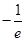 |
已知函数f(x)=-aln x+ +x(a≠0),
+x(a≠0),
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线x-2y=0垂直,求实数a的值;
(2)讨论函数f(x)的单调性.
已知函数f(x)= ,且f(x)的图象在x=1处与直线y=2相切.
,且f(x)的图象在x=1处与直线y=2相切.
(1)求函数f(x)的解析式;
(2)若P(x0,y0)为f(x)图象上的任意一点,直线l与f(x)的图象切于P点,求直线l的斜率k的取值范围.
已知函数f(x)=ax3-3ax,g(x)=bx2+clnx,且g(x)在点(1,g(1))处的切线方程为2y-1=0.
(1)求g(x)的解析式;
(2)设函数G(x)= 若方程G(x)=a2有且仅有四个解,求实数a的取值范围.
若方程G(x)=a2有且仅有四个解,求实数a的取值范围.
设函数 .
.
(Ⅰ)当 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅲ)在(Ⅱ)的条件下,设函数 ,若对于
,若对于 ,
, ,使
,使 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知函数f(x)=k(x﹣1)ex+x2.
(Ⅰ)当时k=﹣ ,求函数f(x)在点(1,1)处的切线方程;
,求函数f(x)在点(1,1)处的切线方程;
(Ⅱ)若在y轴的左侧,函数g(x)=x2+(k+2)x的图象恒在f(x)的导函数f′(x)图象的上方,求k的取值范围;
(Ⅲ)当k≤﹣l时,求函数f(x)在[k,1]上的最小值m.
已知函数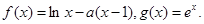
(1)求函数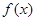 的单调区间;
的单调区间;
(2)当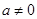 时,过原点分别作曲线
时,过原点分别作曲线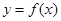 和
和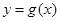 的切线
的切线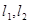 ,已知两切线的斜率互为倒数,证明:
,已知两切线的斜率互为倒数,证明: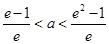 ;
;
(3)设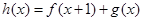 ,当
,当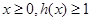 时,求实数
时,求实数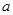 的取值范围.
的取值范围.
已知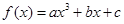 图像过点
图像过点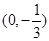 ,且在
,且在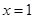 处的切线方程是
处的切线方程是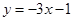 .
.
(1)求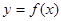 的解析式;
的解析式;
(2)求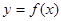 在区间
在区间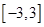 上的最大值和最小值.
上的最大值和最小值.
已知函数 ,其中
,其中 .
.
(1)当 时,求函数
时,求函数 在
在 处的切线方程;
处的切线方程;
(2)若函数 在区间(1,2)上不是单调函数,试求
在区间(1,2)上不是单调函数,试求 的取值范围;
的取值范围;
(3)已知 ,如果存在
,如果存在 ,使得函数
,使得函数
 在
在 处取得最小值,试求
处取得最小值,试求 的最大值.
的最大值.