[广东]2013-2014学年广东惠州高二第一学期期末考试文科数学试卷
某企业为了监控产品质量,从产品流转均匀的生产线上每间隔10分钟抽取一个样本进行检测,这种抽样方法是( )
| A.抽签法 | B.随机数表法 | C.系统抽样法 | D.分层抽样法 |
来源:2013-2014学年广东惠州高二第一学期期末考试文科数学试卷
已知点 是抛物线
是抛物线 的焦点,点
的焦点,点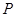 在该抛物线上,且点
在该抛物线上,且点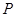 的横坐标是
的横坐标是 ,则
,则 =( )
=( )
| A.2 | B.3 | C.4 | D.5 |
来源:2013-2014学年广东惠州高二第一学期期末考试文科数学试卷
已知事件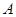 与事件
与事件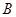 发生的概率分别为
发生的概率分别为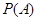 、
、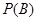 ,有下列命题:
,有下列命题:
①若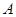 为必然事件,则
为必然事件,则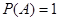 ; ②若
; ②若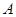 与
与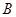 互斥,则
互斥,则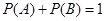 ;
;
③若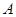 与
与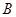 互斥,则
互斥,则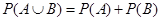 .
.
其中真命题有( )个
| A.0 | B.1 | C.2 | D.3 |
来源:2013-2014学年广东惠州高二第一学期期末考试文科数学试卷
“ ”是“方程
”是“方程 表示的曲线为抛物线”的( )条件
表示的曲线为抛物线”的( )条件
| A.充分不必要 | B.必要不充分 | C.充要 | D.既不充分也不必要 |
来源:2013-2014学年广东惠州高二第一学期期末考试文科数学试卷
已知椭圆
 ,左右焦点分别为
,左右焦点分别为 ,
, ,过
,过 的直线交椭圆于
的直线交椭圆于 两点,若
两点,若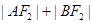 的最大值为8,则
的最大值为8,则 的值是( )
的值是( )
A. |
B. |
C. |
D. |
来源:2013-2014学年广东惠州高二第一学期期末考试文科数学试卷
某城市近10年居民的年收入 与支出
与支出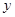 之间的关系大致符合
之间的关系大致符合 (单位:亿元),预计今年该城市居民年收入为20亿元,则今年支出估计是 亿元.
(单位:亿元),预计今年该城市居民年收入为20亿元,则今年支出估计是 亿元.
来源:2013-2014学年广东惠州高二第一学期期末考试文科数学试卷
某社团组织20名志愿者利用周末和节假日参加社会公益活动,志愿者中,年龄在20至40岁的有12人,年龄大于40岁的有8人.
(1)在志愿者中用分层抽样方法随机抽取5名,年龄大于40岁的应该抽取几名?
(2)上述抽取的5名志愿者中任取2名,求取出的2人中恰有1人年龄大于40岁的概率.
来源:2013-2014学年广东惠州高二第一学期期末考试文科数学试卷
设命题 :实数
:实数 满足
满足 ,其中
,其中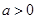 ;命题
;命题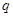 :实数
:实数 满足
满足 .
.
(1)若 ,且
,且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(2)若 是
是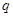 成立的必要不充分条件,求实数
成立的必要不充分条件,求实数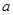 的取值范围.
的取值范围.
来源:2013-2014学年广东惠州高二第一学期期末考试文科数学试卷
已知椭圆
 的离心率为
的离心率为 ,直线
,直线 与圆
与圆 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)设直线 与椭圆
与椭圆 的交点为
的交点为 ,求弦长
,求弦长 .
.
来源:2013-2014学年广东惠州高二第一学期期末考试文科数学试卷
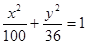 的焦距等于( )
的焦距等于( )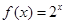 ,则
,则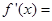 ( )
( )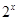
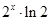


 ”的否定是( )
”的否定是( )



 的单调递增区间为( )
的单调递增区间为( ) 和
和



 ,那么输出
,那么输出 ( )
( )
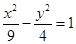 的渐近线方程为 .
的渐近线方程为 .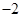 ,
,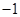 ,
, ,
,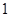 ,
, 的方差为 .
的方差为 . 在
在 处的切线方程是 .
处的切线方程是 . ,
,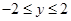 ,点
,点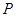 的坐标为
的坐标为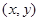 .
. 时,点
时,点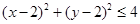 的概率;
的概率; 时,点
时,点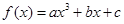 图像过点
图像过点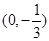 ,且在
,且在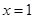 处的切线方程是
处的切线方程是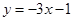 .
.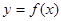 的解析式;
的解析式;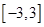 上的最大值和最小值.
上的最大值和最小值. 与椭圆
与椭圆
 交于
交于
 、
、
 两不同点,且△
两不同点,且△ 的面积
的面积 =
= ,其中
,其中 为坐标原点.
为坐标原点. 和
和 均为定值;
均为定值; 的中点为
的中点为 ,求
,求 的最大值;
的最大值; 上是否存在点
上是否存在点 ,使得
,使得 ?若存在,判断△
?若存在,判断△ 的形状;若不存在,请说明理由.
的形状;若不存在,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号