[湖南]2012届湖南省衡阳市高三12月六校联考理科数学试卷
给定性质: ①最小正周期为π;②图象关于直线x= 对称,则下列四个函数中,
对称,则下列四个函数中,
同时具有性质①、②的是( )
A.y = sin( + + ) ) |
B.y = sin(2x- ) ) |
C.y = sin(2x+ ) ) |
D.y = sin|x| |
已知等差数列 的前n项和为
的前n项和为 ,若M、N、P三点共线,O为坐标原点,且
,若M、N、P三点共线,O为坐标原点,且 (直线MP不过点O),则S20等于( )
(直线MP不过点O),则S20等于( )
| A.10 | B.15 | C.20 | D.40 |
定义域为[ ]的函数
]的函数 图像的两个端点为A、B,M(x,y)是
图像的两个端点为A、B,M(x,y)是 图象上任意一点,其中
图象上任意一点,其中 .已知向量
.已知向量 ,若不等式
,若不等式 恒成立, 则称函数
恒成立, 则称函数 在[
在[ ]上“k阶线性近似”.若函数
]上“k阶线性近似”.若函数 在[1,2]上“k阶线性近似”,则实数k的取值范围为( )
在[1,2]上“k阶线性近似”,则实数k的取值范围为( )
A.[0,+∞) B. C.
C. D.
D.
已知函数f(x)=|x-2|,若a≠0,且a,b∈R,都有不等式|a+b|+|a-b|≥|a|·f(x)成立,则实数x的取值范围是 .
如图,一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是 .
在一个数列中,如果 ,都有
,都有 (
( 为常数),那么这个数列
为常数),那么这个数列
叫做等积数列, 叫做这个数列的公积。已知数列
叫做这个数列的公积。已知数列 是等积数列,且
是等积数列,且 ,公
,公
积为8,则 .
.
当 时,定义函数
时,定义函数 表示n的最大奇因数.如
表示n的最大奇因数.如 ,
, ,记
,记
 则(1)S(3)=___________;(2)S(n)=___________.
则(1)S(3)=___________;(2)S(n)=___________.
(本小题满分12分)
已知向量
 ,
,
 ,函数
,函数

(1)若 ,求
,求 的值;
的值;
(2)在△ABC中,角A,B,C的对边分别是 ,且满足
,且满足 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)已知 平面
平面 ,
, 平面
平面 ,△
,△ 为等边三角形,边长为2a,
为等边三角形,边长为2a, ,
, 为
为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 ;
;
(3)求直线 和平面
和平面 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)
已知数列 满足条件:
满足条件: ,
,
(1)判断数列 是否为等比数列;
是否为等比数列;
(2)若 ,令
,令 , 记
, 记
证明:(ⅰ) ; (ⅱ)
; (ⅱ)
(本小题满分13分)
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车
流速度v(单位:千米/小时)是车流密度 x(单位:辆/千米)的函数.当桥上的车流密度达
到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速
度为60千米/小时.研究表明当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值.(精确到1辆/小时)
(本小题满分13分)
已知函数 ,
, ,其中
,其中 R.
R.
(1)当a=1时,判断 的单调性;
的单调性;
(2)若 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围;
(3)设函数 ,当
,当 时,若
时,若 ,
, ,总有
,总有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 则
则 的值是 ( )
的值是 ( )

 且
且 则
则 ( )
( )



 的否定是( )
的否定是( )


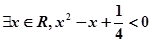
 是
是 上的偶函数,若对于
上的偶函数,若对于 ,都有
,都有 ,且当
,且当 时,
时, ,则
,则 ( )
( )


 满足条件
满足条件 则该目标函数
则该目标函数 的最大值为 ( )
的最大值为 ( )
 极轴为
极轴为 轴正半轴
轴正半轴 是
是 的外接圆,过点
的外接圆,过点 的切线交
的切线交 的延长线于点
的延长线于点 ,
, ,则
,则 的长为 .
的长为 .
 ,且
,且 是第二象限角,则
是第二象限角,则 = .
= . 的边长为
的边长为 ,平面内一点
,平面内一点 满足
满足 , 则
, 则 .
. ,数列
,数列 和
和 满足:
满足: ,
, ,函数
,函数 的图像在点
的图像在点 处的切线在
处的切线在 轴上的截距为
轴上的截距为 .
.  }的通项公式;
}的通项公式; 的项中仅
的项中仅 最小,求
最小,求 的取值范围;
的取值范围; ,令函数
,令函数 数列
数列 满足:
满足: 且
且 证明:
证明:
 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号