(本小题满分14分)如图,已知 中,
中,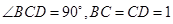 ,
,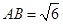 ,
,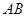 ⊥
⊥
平面 ,
,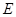 、
、 分别是
分别是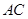 、
、 的中点.
的中点.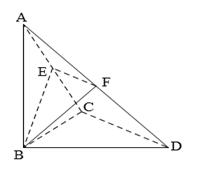
(1)求证:平面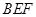 ⊥平面
⊥平面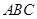 ;
;
(2)设平面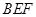
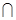 平面
平面 ,求证
,求证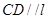 ;
;
(3)求四棱锥B-CDFE的体积V.
如图,在正方体ABCD-A1B1C1D1中.

(1)若E为棱DD1上的点,试确定点E的位置,使平面A1C1E∥B1D;
(2)若M为A1B上的一动点,求证:DM∥平面D1B1C.
(本小题满分14分)如图, 是边长为
是边长为 的等边三角形,
的等边三角形, 是等腰直角三角形,
是等腰直角三角形, ,平面
,平面
 平面
平面 ,且
,且 平面
平面 ,
, .
.
(1)证明: 平面
平面 ;
;
(2)证明:
 .
.
(本小题满分14分)如图,在四棱锥P - ABCD中,四边形ABCD是矩形,平面PCD⊥平面ABCD,M为PC中点.求证:
(1)PA∥平面MDB;
(2)PD⊥BC.
(本小题满分12分)如图,在长方体 中,
中, 为
为 的中点.
的中点.
(Ⅰ)求证: ;
;
(Ⅱ)在棱 上是否存在点
上是否存在点 ,使得
,使得 ∥平面
∥平面 ?若存在,求出
?若存在,求出 的长;若不存在,说明理由.
的长;若不存在,说明理由.
(本小题满分15分)如图,在四棱锥 中,底面
中,底面 是平行四边形,
是平行四边形, 平面
平面 ,点
,点 分别为
分别为 的中点,且
的中点,且 ,
, ,
, .
.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正切值.
所成角的正切值.
如图,在三棱柱 中,四边形
中,四边形 都为矩形.
都为矩形.
(I)设D是AB的中点,证明:直线 平面
平面 ;
;
(II)在 中,若
中,若 ,证明:直线
,证明:直线 平面
平面 .
.
如图,四棱锥 中,四边形
中,四边形 是正方形,若
是正方形,若 分别是线段
分别是线段 的中点.
的中点.
(1)求证: ||底面
||底面 ;
;
(2)若点 为线段
为线段 的中点,平面
的中点,平面 与平面
与平面 有怎样的位置关系?并证明。
有怎样的位置关系?并证明。