(本小题满分12分)如图,三棱柱 中,平面
中,平面 平面
平面 ,四边形
,四边形 是矩形,
是矩形, ,
, 分别为
分别为 的中点.
的中点.
(1)求证: ∥平面
∥平面 ;
;
(2)求点 到平面
到平面 的距离
的距离 .
.
(本小题满分9分)如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=a.
(1)求证:MN∥平面PAD;
(2)求证:平面PMC⊥平面PCD.
如图,四边形ABEF是等腰梯形,AB∥EF,AF=BE=2,EF=4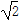 ,AB=2
,AB=2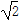 ,ABCD是矩形.AD⊥平面ABEF,其中Q,M分别是AC,EF的中点,P是BM中点.
,ABCD是矩形.AD⊥平面ABEF,其中Q,M分别是AC,EF的中点,P是BM中点.
(1)求证:PQ∥平面BCE;
(2)求证:AM⊥平面BCM;
(3)求点F到平面BCE的距离.
(本小题满分14分)如图,在五面体 中,四边形
中,四边形 是边长为4的正方形,
是边长为4的正方形, ,平面
,平面
 平面
平面 ,且
,且 ,
, ,点G是EF的中点.
,点G是EF的中点.
(Ⅰ)证明:
 平面
平面 ;
;
(Ⅱ)若直线BF与平面 所成角的正弦值为
所成角的正弦值为 ,求
,求 的长;
的长;
(Ⅲ)判断线段 上是否存在一点
上是否存在一点 ,使
,使 //平面
//平面 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
如图,在多面体 中,四边形
中,四边形 是菱形,
是菱形, 相交于点
相交于点 ,
, ,
, ,平面
,平面
 平面
平面 ,
, ,点
,点 为
为 的中点.
的中点.
(1)求证:直线 平面
平面 ;
;
(2)求证:直线
 平面
平面 .
.
如图所示,已知空间四边形 的每条边和对角线长都等于1,点
的每条边和对角线长都等于1,点 ,
, ,
, 分别是
分别是 、
、 、
、 的中点,计算:
的中点,计算:
(1) ;
;
(2) 的长;
的长;
(3)异面直线 与
与 所成角的余弦值.
所成角的余弦值.
(本小题满分12分)如图,三棱台 中,
中, 分别为
分别为 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)若 求证:平面
求证:平面 平面
平面 .
.
(本小题满分12分)已知三棱柱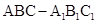 中,侧棱垂直于底面,
中,侧棱垂直于底面,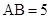 ,
,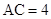 ,
,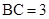 ,
, ,点
,点 在
在 上.
上.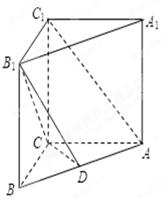
(1)若 是
是 中点,求证:
中点,求证: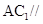 平面
平面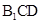 ;
;
(2)当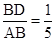 时,求二面角
时,求二面角 的余弦值.
的余弦值.
(本小题满分12分)如图, 垂直于梯形
垂直于梯形 所在的平面,
所在的平面, .
. 为
为 中点,
中点, ,
, 四边形
四边形 为矩形,线段
为矩形,线段 交
交 于点N .
于点N .

(1)求证: // 平面
// 平面 ;
;
(2)求二面角 的大小;
的大小;
(3)在线段 上是否存在一点
上是否存在一点 ,使得
,使得 与平面
与平面 所成角的大小为
所成角的大小为 ? 若存在,请求出
? 若存在,请求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.