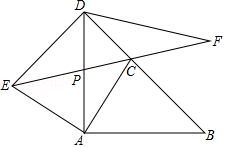
如图,在正方形 中,点 在 边上,连接 , 的平分线 与 边交于点 ,与 的延长线交于点 .设 .
(1)若 , ,求线段 的长.
(2)连接 ,若 ,
①求证:点 为 边的中点.
②求 的值.

设函数 , .
(1)当 时,函数 的最大值是 ,函数 的最小值是 ,求 和 的值.
(2)设 ,且 ,当 时, ;当 时, .圆圆说:“ 一定大于 ”.你认为圆圆的说法正确吗?为什么?
如图,在 中,点 , , 分别在 , , 边上, , .
(1)求证: .
(2)设 ,
①若 ,求线段 的长;
②若 的面积是20,求 的面积.

某工厂生产某种产品,3月份的产量为5000件,4月份的产量为10000件.用简单随机抽样的方法分别抽取这两个月生产的该产品若干件进行检测,并将检测结果分别绘制成如图所示的扇形统计图和频数直方图(每组不含前一个边界值,含后一个边界值).已知检测综合得分大于70分的产品为合格产品.
(1)求4月份生产的该产品抽样检测的合格率;
(2)在3月份和4月份生产的产品中,估计哪个月的不合格件数多?为什么?

以下是圆圆解方程 的答案过程.
解:去分母,得 .
去括号,得 .
移项,合并同类项,得 .
圆圆的答案过程是否有错误?如果有错误,写出正确的答案过程.
在平面直角坐标系中,已知点 , , ,直线 经过点 ,抛物线 恰好经过 , , 三点中的两点.
(1)判断点 是否在直线 上,并说明理由;
(2)求 , 的值;
(3)平移抛物线 ,使其顶点仍在直线 上,求平移后所得抛物线与 轴交点纵坐标的最大值.
某单位食堂为全体960名职工提供了 , , , 四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取240名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查.根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:

(1)在抽取的240人中最喜欢 套餐的人数为 ,扇形统计图中“ ”对应扇形的圆心角的大小为 ;
(2)依据本次调查的结果,估计全体960名职工中最喜欢 套餐的人数;
(3)现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,求甲被选到的概率.
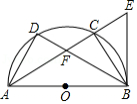
如图, 是半圆 的直径, , 是半圆 上不同于 , 的两点, , 与 相交于点 . 是半圆 所在圆的切线,与 的延长线相交于点 .
(1)求证: ;
(2)若 ,求证: 平分 .
某超市有线上和线下两种销售方式.与2019年4月份相比,该超市2020年4月份销售总额增长 ,其中线上销售额增长 ,线下销售额增长 .
(1)设2019年4月份的销售总额为 元,线上销售额为 元,请用含 , 的代数式表示2020年4月份的线下销售额(直接在表格中填写结果);
时间 |
销售总额(元 |
线上销售额(元 |
线下销售额(元 |
2019年4月份 |
|
|
|
2020年4月份 |
|
|
|
(2)求2020年4月份线上销售额与当月销售总额的比值.
如图,山顶上有一个信号塔 ,已知信号塔高 米,在山脚下点 处测得塔底 的仰角 ,塔顶 的仰角 ,求山高 (点 , , 在同一条竖直线上).
(参考数据: , , .

观察以下等式:
第1个等式: ,
第2个等式: ,
第3个等式: ,
第4个等式: .
第5个等式: .
按照以上规律,解决下列问题:
(1)写出第6个等式: ;
(2)写出你猜想的第 个等式: (用含 的等式表示),并证明.
如图,在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为端点的线段 ,线段 在网格线上.
(1)画出线段 关于线段 所在直线对称的线段 (点 , 分别为 , 的对应点);
(2)将线段 绕点 顺时针旋转 得到线段 ,画出线段 .

如图, 由 绕点 按逆时针方向旋转 得到,且点 的对应点 恰好落在 的延长线上, , 相交于点 .
(1)求 的度数;
(2) 是 延长线上的点,且 .
①判断 和 的数量关系,并证明;
②求证: .