初中数学解直角三角形的应用-仰角俯角问题试题

济南大明湖畔的“超然楼”被称作“江北第一楼”，某校数学社团的同学对超然楼的高度进行了测量，如图，他们在 $A$处仰望塔顶，测得仰角为 $30°$，再往楼的方向前进 $60m$至 $B$处，测得仰角为 $60°$，若学生的身高忽略不计， $\sqrt{3}\approx 1.7$，结果精确到 $1m$，则该楼的高度 $\mathit{CD}$为 $($　　 $)$

A． $47m$B． $51m$C． $53m$D． $54m$

2016年2月1日，我国在西昌卫星发射中心，用长征三号丙运载火箭成功将第5颗新一代北斗星送入预定轨道，如图，火箭从地面 $L$处发射，当火箭达到 $A$点时，从位于地面 $R$处雷达站测得 $\mathit{AR}$的距离是 $6\mathit{km}$，仰角为 $42.4°$；1秒后火箭到达 $B$点，此时测得仰角为 $45.5°$

（1）求发射台与雷达站之间的距离 $\mathit{LR}$；

（2）求这枚火箭从 $A$到 $B$的平均速度是多少（结果精确到 $0.01)$？

（参考数据： $\sin 42.4°\approx 0.67$， $\cos 42.4°\approx 0.74$， $\tan 42.4°\approx 0.905$， $\sin 45.5°\approx 0.71$， $\cos 45.5°\approx 0.70$， $\tan 45.5°\approx 1.02)$

如图，从楼 $\mathit{AB}$的 $A$处测得对面楼 $\mathit{CD}$的顶部 $C$的仰角为 $37°$，底部 $D$的俯角为 $45°$，两楼的水平距离 $\mathit{BD}$为 $24m$，那么楼 $\mathit{CD}$的高度约为　　 $m$．（结果精确到 $1m$，参考数据： $\sin 37°\approx 0.6$； $\cos 37°\approx 0.8$； $\tan 37°\approx 0.75)$

如图，某城市的电视塔 $\mathit{AB}$坐落在湖边，数学老师带领学生隔湖测量电视塔 $\mathit{AB}$的高度，在点 $M$处测得塔尖点 $A$的仰角 $\angle \mathit{AMB}$为 $22.5°$，沿射线 $\mathit{MB}$方向前进200米到达湖边点 $N$处，测得塔尖点 $A$在湖中的倒影 $A\text{'}$的俯角 $\angle A\text{'}\mathit{NB}$为 $45°$，则电视塔 $\mathit{AB}$的高度为　　米（结果保留根号）．

小明在热气球 $A$上看到正前方横跨河流两岸的大桥 $\mathit{BC}$，并测得 $B$， $C$两点的俯角分别为 $53°$和 $45°$，已知大桥 $\mathit{BC}$与地面在同一水平面上，其长度为 $75m$，请求出热气球离地面的高度．（参考数据： $\sin 53°\approx \frac{4}{5}$， $\cos 53°\approx \frac{3}{5}$， $\tan 53°\approx \frac{4}{3})$．

如图， $\mathit{AB}$是某景区内高 $10m$的观景台， $\mathit{CD}$是与 $\mathit{AB}$底部相平的一座雕像（含底座），在观景台顶 $A$处测得雕像顶 $C$点的仰角为 $30°$，从观景台底部 $B$处向雕像方向水平前进 $6m$到达点 $E$，在 $E$处测得雕像顶 $C$点的仰角为 $60°$，已知雕像底座 $\mathit{DF}$高 $8m$，求雕像 $\mathit{CF}$的高．（结果保留根号）

如图，聪聪想在自己家的窗口 $A$处测量对面建筑物 $\mathit{CD}$的高度，他首先量出窗口 $A$到地面的距离 $\left(\mathit{AB}\right)$为 $16m$，又测得从 $A$处看建筑物底部 $C$的俯角 $\alpha$为 $30°$，看建筑物顶部 $D$的仰角 $\beta$为 $53°$，且 $\mathit{AB}$， $\mathit{CD}$都与地面垂直，点 $A$， $B$， $C$， $D$在同一平面内．

（1）求 $\mathit{AB}$与 $\mathit{CD}$之间的距离（结果保留根号）．

（2）求建筑物 $\mathit{CD}$的高度（结果精确到 $1m)$．

（参考数据： $\sin 53°\approx 0.8$， $\cos 53°\approx 0.6$， $\tan 53\approx 1.3$， $\sqrt{3}\approx 1.7)$

如图，小明在教学楼 $A$处分别观测对面实验楼 $\mathit{CD}$底部的俯角为 $45°$，顶部的仰角为 $37°$，已知教学楼和实验楼在同一平面上，观测点距地面的垂直高度 $\mathit{AB}$为 $15m$，求实验楼的垂直高度即 $\mathit{CD}$长（精确到 $1m)$

参考值： $\sin 37°=0.60$， $\cos 37°=0.80$， $\tan 37°=0.75$．

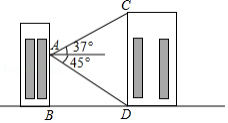
如图所示，飞机在一定高度上沿水平直线飞行，先在点 $A$处测得正前方小岛 $C$的俯角为 $30°$，面向小岛方向继续飞行 $10\mathit{km}$到达 $B$处，发现小岛在其正后方，此时测得小岛的俯角为 $45°$，如果小岛高度忽略不计，求飞机飞行的高度（结果保留根号）．

热气球的探测器显示，从热气球 $A$看一栋楼顶部 $B$的仰角 $\alpha$为 $45°$，看这栋楼底部 $C$的俯角 $\beta$为 $60°$，热气球与楼的水平距离为 $100m$，求这栋楼的高度（结果保留根号）．

如图，为了测出旗杆 $\mathit{AB}$的高度，在旗杆前的平地上选择一点 $C$，测得旗杆顶部 $A$的仰角为 $45°$，在 $C$、 $B$之间选择一点 $D(C$、 $D$、 $B$三点共线），测得旗杆顶部 $A$的仰角为 $75°$，且 $\mathit{CD}=8m$

（1）求点 $D$到 $\mathit{CA}$的距离；

（2）求旗杆 $\mathit{AB}$的高．

（注 $:$结果保留根号）

如图，地面上两个村庄 $C$、 $D$处于同一水平线上，一飞行器在空中以6千米 $/$小时的速度沿 $\mathit{MN}$方向水平飞行，航线 $\mathit{MN}$与 $C$、 $D$在同一铅直平面内．当该飞行器飞行至村庄 $C$的正上方 $A$处时，测得 $\angle \mathit{NAD}=60°$；该飞行器从 $A$处飞行40分钟至 $B$处时，测得 $\angle \mathit{ABD}=75°$．求村庄 $C$、 $D$间的距离 $(\sqrt{3}$取1.73，结果精确到0.1千米）

如图，为了测量某建筑物 $\mathit{MN}$的高度，在平地上 $A$处测得建筑物顶端 $M$的仰角为 $30°$，向 $N$点方向前进 $16m$到达 $B$处，在 $B$处测得建筑物顶端 $M$的仰角为 $45°$，则建筑物 $\mathit{MN}$的高度等于 $($　　 $)$

A． $8(\sqrt{3}+1)m$B． $8(\sqrt{3}-1)m$C． $16(\sqrt{3}+1)m$D． $16(\sqrt{3}-1)m$

如图，某学校体育场看台的顶端 $C$到地面的垂直距离 $\mathit{CD}$为 $2m$，看台所在斜坡 $\mathit{CM}$的坡比 $i=1:3$，在点 $C$处测得旗杆顶点 $A$的仰角为 $30°$，在点 $M$处测得旗杆顶点 $A$的仰角为 $60°$，且 $B$， $M$， $D$三点在同一水平线上，求旗杆 $\mathit{AB}$的高度．（结果精确到 $0.1m$，参考数据： $\sqrt{2}\approx 1.41$， $\sqrt{3}=1.73)$

如图，学校教学楼上悬挂一块长为 $3m$的标语牌，即 $\mathit{CD}=3m$．数学活动课上，小明和小红要测量标语牌的底部点 $D$到地面的距离．测角仪支架高 $\mathit{AE}=\mathit{BF}=1.2m$，小明在 $E$处测得标语牌底部点 $D$的仰角为 $31°$，小红在 $F$处测得标语牌顶部点 $C$的仰角为 $45°$， $\mathit{AB}=5m$，依据他们测量的数据能否求出标语牌底部点 $D$到地面的距离 $\mathit{DH}$的长？若能，请计算；若不能，请说明理由（图中点 $A$， $B$， $C$， $D$， $E$， $F$， $H$在同一平面内）

（参考数据： $\tan 31°\approx 0.60$， $\sin 31°\approx 0.52$， $\cos 31°\approx 0.86)$