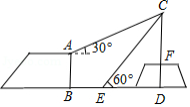
如图, 是某景区内高 的观景台, 是与 底部相平的一座雕像(含底座),在观景台顶 处测得雕像顶 点的仰角为 ,从观景台底部 处向雕像方向水平前进 到达点 ,在 处测得雕像顶 点的仰角为 ,已知雕像底座 高 ,求雕像 的高.(结果保留根号)
相关知识点
推荐套卷
如图, 是某景区内高 的观景台, 是与 底部相平的一座雕像(含底座),在观景台顶 处测得雕像顶 点的仰角为 ,从观景台底部 处向雕像方向水平前进 到达点 ,在 处测得雕像顶 点的仰角为 ,已知雕像底座 高 ,求雕像 的高.(结果保留根号)
