初中数学解直角三角形的应用-仰角俯角问题试题

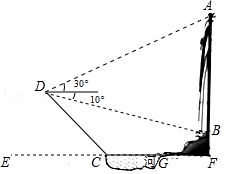
数学“综合与实践”课中，老师带领同学们来到娄底市郊区，测算如图所示的仙女峰的高度，李红盛同学利用已学的数学知识设计了一个实践方案，并实施了如下操作：先在水平地面 $A$处测得山顶 $B$的仰角 $\angle \mathit{BAC}$为 $38.7°$，再由 $A$沿水平方向前进377米到达山脚 $C$处，测得山坡 $\mathit{BC}$的坡度为 $1:0.6$，请你求出仙女峰的高度（参考数据： $\tan 38.7°\approx 0.8)$

衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内，如图，为了测量来雁塔的高度，在 $E$处用高为1.5米的测角仪 $\mathit{AE}$，测得塔顶 $C$的仰角为 $30°$，再向塔身前进10.4米，又测得塔顶 $C$的仰角为 $60°$，求来雁塔的高度．（结果精确到0.1米）

如图，有一铁塔 $\mathit{AB}$，为了测量其高度，在水平面选取 $C$， $D$两点，在点 $C$处测得 $A$的仰角为 $45°$，距点 $C$的10米 $D$处测得 $A$的仰角为 $60°$，且 $C$、 $D$、 $B$在同一水平直线上，求铁塔 $\mathit{AB}$的高度（结果精确到0.1米， $\sqrt{3}\approx 1.732)$

乌江快铁大桥是快铁渝黔线的一项重要工程，由主桥 $\mathit{AB}$和引桥 $\mathit{BC}$两部分组成（如图所示），建造前工程师用以下方式做了测量：无人机在 $A$处正上方 $97m$处的 $P$点，测得 $B$处的俯角为 $30°$（当时 $C$处被小山体阻挡无法观测）．无人机飞行到 $B$处正上方的 $D$处时能看到 $C$处，此时测得 $C$处俯角为 $80°36\text{'}$．

（1）求主桥 $\mathit{AB}$的长度；

（2）若两观察点 $P$、 $D$的连线与水平方向的夹角为 $30°$，求引桥 $\mathit{BC}$的长．

（长度均精确到 $1m$，参考数据： $\sqrt{3}\approx 1.73$， $\sin 80°36\text{'}\approx 0.987$， $\cos 80°36\text{'}\approx 0.163$， $\tan 80°36\text{'}\approx 6.06)$

阅读材料：

一般地，当 $\alpha$、 $\beta$为任意角时， $\tan (\alpha +\beta )$与 $\tan (\alpha -\beta )$的值可以用下面的公式求得： $\tan (\alpha \pm \beta )=\frac{\tan \alpha \pm \tan \beta }{1\pm \tan \alpha ·\tan \beta }$．

例如： $\tan 15°=\tan (45°-30°)=\frac{\tan 45°-\tan 30°}{1+\tan 45°·\tan 30°}=\frac{1-\frac{\sqrt{3}}{3}}{1+1\times \frac{\sqrt{3}}{3}}=\frac{(3-\sqrt{3})}{(3+\sqrt{3})}$

$=\frac{(3-\sqrt{3})(3-\sqrt{3})}{(3+\sqrt{3})(3-\sqrt{3})}=\frac{12-6\sqrt{3}}{6}=2-\sqrt{3}$．

根据以上材料，解决下列问题：

（1）求 $\tan 75°$的值；

（2）都匀文峰塔，原名文笔塔，始建于明代万历年间，系五层木塔．文峰塔的木塔年久倾毁，仅存塔基．1983年，人民政府拨款维修文峰塔，成为今天的七层六面实心石塔（图 $1)$，小华想用所学知识来测量该铁塔的高度，如图2，已知小华站在离塔底中心 $A$处5.7米的 $C$处，测得塔顶的仰角为 $75°$，小华的眼睛离地面的距离 $\mathit{DC}$为1.72米，请帮助小华求出文峰塔 $\mathit{AB}$的高度．（精确到1米，参考数据 $\sqrt{3}\approx 1.732$， $\sqrt{2}\approx 1.414)$

黔东南州某校吴老师组织九（1）班同学开展数学活动，带领同学们测量学校附近一电线杆的高．已知电线杆直立于地面上，某天在太阳光的照射下，电线杆的影子（折线 $\mathit{BCD})$恰好落在水平地面和斜坡上，在 $D$处测得电线杆顶端 $A$的仰角为 $30°$，在 $C$处测得电线杆顶端 $A$得仰角为 $45°$，斜坡与地面成 $60°$角， $\mathit{CD}=4m$，请你根据这些数据求电线杆的高 $\left(\mathit{AB}\right)$．

（结果精确到 $1m$，参考数据： $\sqrt{2}\approx 1.4$， $\sqrt{3}\approx 1.7)$

随着人们生活水平的不断提高，旅游已成为人们的一种生活时尚．为开发新的旅游项目，我市对某山区进行调查，发现一瀑布．为测量它的高度，测量人员在瀑布的对面山上 $D$点处测得瀑布顶端 $A$点的仰角是 $30°$，测得瀑布底端 $B$点的俯角是 $10°$， $\mathit{AB}$与水平面垂直．又在瀑布下的水平面测得 $\mathit{CG}=27m$， $\mathit{GF}=17.6m$（注 $:C$、 $G$、 $F$三点在同一直线上， $\mathit{CF}\perp \mathit{AB}$于点 $F)$．斜坡 $\mathit{CD}=20m$，坡角 $\angle \mathit{ECD}=40°$．求瀑布 $\mathit{AB}$的高度．

（参考数据： $\sqrt{3}\approx 1.73$， $\sin 40°\approx 0.64$， $\cos 40°\approx 0.77$， $\tan 40°\approx 0.84$， $\sin 10°\approx 0.17$， $\cos 10°\approx 0.98$， $\tan 10°\approx 0.18)$

小菁同学在数学实践活动课中测量路灯的高度．如图，已知她的目高 $\mathit{AB}$为1.5米，她先站在 $A$处看路灯顶端 $O$的仰角为 $35°$，再往前走3米站在 $C$处，看路灯顶端 $O$的仰角为 $65°$，则路灯顶端 $O$到地面的距离约为（已知 $\sin 35°\approx 0.6$， $\cos 35°\approx 0.8$， $\tan 35°\approx 0.7$， $\sin 65°\approx 0.9$， $\cos 65°\approx 0.4$， $\tan 65°\approx 2.1\left)\right($　　 $)$

A．3.2米B．3.9米C．4.7米D．5.4米

如图，斜坡 $\mathit{BE}$，坡顶 $B$到水平地面的距离 $\mathit{AB}$为3米，坡底 $\mathit{AE}$为18米，在 $B$处， $E$处分别测得 $\mathit{CD}$顶部点 $D$的仰角为 $30°$， $60°$，求 $\mathit{CD}$的高度．（结果保留根号）

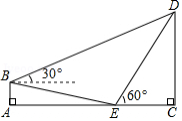
如图， $\mathit{CD}$是一高为4米的平台， $\mathit{AB}$是与 $\mathit{CD}$底部相平的一棵树，在平台顶 $C$点测得树顶 $A$点的仰角 $\alpha =30°$，从平台底部向树的方向水平前进3米到达点 $E$，在点 $E$处测得树顶 $A$点的仰角 $\beta =60°$，求树高 $\mathit{AB}$（结果保留根号）

如图，埃航 $\mathit{MS}804$客机失事后，国家主席亲自发电进行慰问，埃及政府出动了多艘舰船和飞机进行搜救，其中一艘潜艇在海面下500米的 $A$点处测得俯角为 $45°$的前下方海底有黑匣子信号发出，继续沿原方向直线航行2000米后到达 $B$点，在 $B$处测得俯角为 $60°$的前下方海底有黑匣子信号发出，求海底黑匣子 $C$点距离海面的深度（结果保留根号）．

如图，为了测量出楼房 $\mathit{AC}$的高度，从距离楼底 $C$处 $60\sqrt{3}$米的点 $D$（点 $D$与楼底 $C$在同一水平面上）出发，沿斜面坡度为 $i=1:\sqrt{3}$的斜坡 $\mathit{DB}$前进30米到达点 $B$，在点 $B$处测得楼顶 $A$的仰角为 $53°$，求楼房 $\mathit{AC}$的高度（参考数据： $\sin 53°\approx 0.8$， $\cos 53°\approx 0.6$， $\tan 53°\approx \frac{4}{3}$，计算结果用根号表示，不取近似值）．

某班数学课外活动小组的同学欲测量公园内一棵树 $\mathit{DE}$的高度，他们在这棵树正前方一楼亭前的台阶上 $A$点处测得树顶端 $D$的仰角为 $30°$，朝着这棵树的方向走到台阶下的点 $C$处测得树顶端 $D$的仰角为 $60°$，已知 $A$点的高度 $\mathit{AB}$为2米，台阶 $\mathit{AC}$的坡度 $i=1:2$，且 $B$， $C$， $E$三点在同一条直线上，请根据以上条件求出树 $\mathit{DE}$的高度．（测倾器的高度忽略不计，结果保留根号）

在学习完“利用三角函数测高”这节内容之后，某兴趣小组开展了测量学校旗杆高度的实践活动，如图，在测点 $A$处安置测倾器，量出高度 $\mathit{AB}=1.5m$，测得旗杆顶端 $D$的仰角 $\angle \mathit{DBE}=32°$，量出测点 $A$到旗杆底部 $C$的水平距离 $\mathit{AC}=20m$，根据测量数据，求旗杆 $\mathit{CD}$的高度．（参考数据： $\sin 32°\approx 0.53$， $\cos 32°\approx 0.85$， $\tan 32°\approx 0.62)$

如图，在一次测量活动中，小丽站在离树底部 $E$处 $5m$的 $B$处仰望树顶 $C$，仰角为 $30°$，已知小丽的眼睛离地面的距离 $\mathit{AB}$为 $1.65m$，那么这棵树大约有多高？（结果精确到 $0.1m$，参考数据： $\sqrt{3}\approx 1.73)$