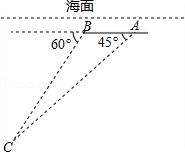
如图,埃航 客机失事后,国家主席亲自发电进行慰问,埃及政府出动了多艘舰船和飞机进行搜救,其中一艘潜艇在海面下500米的 点处测得俯角为 的前下方海底有黑匣子信号发出,继续沿原方向直线航行2000米后到达 点,在 处测得俯角为 的前下方海底有黑匣子信号发出,求海底黑匣子 点距离海面的深度(结果保留根号).
相关知识点
推荐套卷
如图,埃航 客机失事后,国家主席亲自发电进行慰问,埃及政府出动了多艘舰船和飞机进行搜救,其中一艘潜艇在海面下500米的 点处测得俯角为 的前下方海底有黑匣子信号发出,继续沿原方向直线航行2000米后到达 点,在 处测得俯角为 的前下方海底有黑匣子信号发出,求海底黑匣子 点距离海面的深度(结果保留根号).
