等边△ABC边长为6，P为BC边上一点，∠MPN=60°，且PM、PN分别于边AB、AC交于点E、F.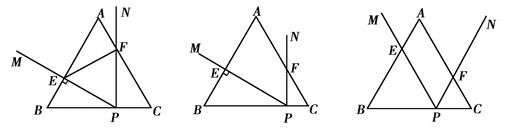
（1）如图1，当点P为BC的三等分点，且PE⊥AB时，判断△EPF的形状；
（2）如图2，若点P在BC边上运动，且保持PE⊥AB，设BP=x，四边形AEPF面积的y，求y与x的函数关系式，并写出自变量x的取值范围；
（3）如图3，若点P在BC边上运动，且∠MPN绕点P旋转，当CF=AE=2时，求PE的长.
相关试题
如图，在△ABC中，AD⊥BC于D，AE平分∠BAC．
（1）若∠C－∠B＝30°，则∠DAE＝________．
（2）若∠C－∠B＝
（∠C＞∠B），求∠DAE的度数（用含的代数式表示）．
相关知识点
推荐套卷
粤公网安备 44130202000953号