如图,已知二次函数y=ax2+bx+8(a≠0)的图像与x轴交于点A(-2,0),B,与y轴交于点C,tan∠ABC=2.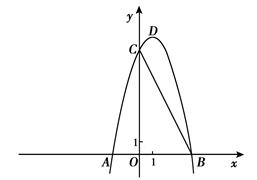
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得经过点P的直线PM垂直于直线CD,且与直线OP的夹角为75°?若存在,求出点P的坐标;若不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴向上平移,使抛物线与线段EF总有公共点.试探究:抛物线最多可以向上平移多少个单位长度?
相关知识点
推荐套卷
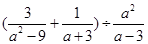 的值.
的值.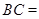
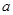 ,
,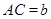 ,
,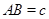 .
.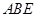 =45°,
=45°,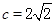 时,
时,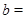 ;
;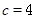 时,
时,
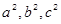 三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;
三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;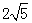 ,AB=3.求AF的长.
,AB=3.求AF的长. 轴分别交于点E, F.
轴分别交于点E, F.
 的最小值为 ;
的最小值为 ; 的增大而减小时,
的增大而减小时, 时,求
时,求 的值,并判断四边形
的值,并判断四边形 的形状(直接写出,不必证明);
的形状(直接写出,不必证明); ,当△
,当△ 为等腰三角形时,求方程
为等腰三角形时,求方程 的解.
的解. (1≤
(1≤ 元.
元.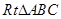 中,
中, ,
,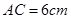 ,
,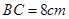 ,动点
,动点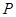 从点
从点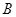 出发,在
出发,在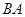 边上以每秒
边上以每秒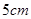 的速度向点
的速度向点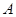 匀速运动,同时动点
匀速运动,同时动点 从点
从点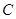 出发,在
出发,在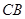 边上以每秒
边上以每秒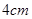 的速度向点
的速度向点 秒(
秒( ),连接
),连接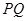 。
。
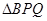 与
与 相似,求
相似,求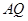 ,
,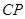 ,若
,若 ,求
,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号