如图,在某街道路边有相距 、高度相同的两盏路灯(灯杆垂直地面),小明为了测量路灯的高度,在地面 处测得路灯 的顶端仰角为 ,向前行走 到达 处,在地面测得路灯 的顶端仰角为 ,已知点 , , , 在同一条直线上,请你利用所学知识帮助小明求出路灯的高度.(结果精确到 .参考数据: , , , , ,

如图,建筑物 上有一杆 .从与 相距 的 处观测旗杆顶部 的仰角为 ,观测旗杆底部 的仰角为 ,则旗杆 的高度约为 (结果取整数,参考数据: , , .

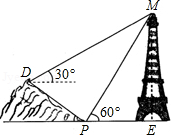
小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚 处测得古塔顶端 的仰角为 ,沿山坡向上走 到达 处,测得古塔顶端 的仰角为 .已知山坡坡度 ,即 ,请你帮助小明计算古塔的高度 .(结果精确到 ,参考数据:
如图,建筑物 的高为52米,在其正前方广场上有人进行航模试飞.从建筑物顶端 处测得航模 的俯角 ,同一时刻从建筑物的底端 处测得航模 的仰角 ,求此时航模 的飞行高度.(精确到1米)
(参考数据: , ,

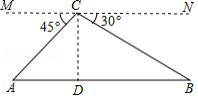
如图,某地质公园中有两座相邻小山.游客需从左侧小山山脚 处乘坐竖直观光电梯上行100米到达山顶 处,然后既可以沿水平观光桥步行到景点 处,也可以通过滑行索道到达景点 处,在山顶 处观测坡底 的俯角为 ,观测 处的俯角为 ,已知右侧小山的坡角为 (图中的点 , , , , , 均在同一平面内,点 , , 在同一直线上)
(1)求 的度数及 的长度;
(2)求 , 两点之间的距离.(结果保留根号)

如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点 处的求救者后,又发现点 正上方点 处还有一名求救者,在消防车上点 处测得点 和点 的仰角分别为 和 ,点 距地面2.5米,点 距地面10.5米,为救出点 处的求救者,云梯需要继续上升的高度 约为多少米?
(结果保留整数,参考数据: , , ,

如图,某景区的两个景点 、 处于同一水平地面上、一架无人机在空中沿 方向水平飞行进行航拍作业, 与 在同一铅直平面内,当无人机飞行至 处时、测得景点 的俯角为 ,景点 的俯角为 ,此时 到地面的距离 为100米,则两景点 、 间的距离为 米(结果保留根号).
如图,在点 处测得塔顶 的仰角为 ,点 到塔底 的水平距离 是 ,那么塔 的高度为 (结果保留根号).

如图,小明利用长为 的标尺 测量某建筑物 的高度,观测点 、标尺底端 与建筑物底端 在同一条水平直线上,标尺 .从点 处测得建筑物顶端 的仰角为 ,此时点 恰好在 上;从点 处测得建筑物顶端 的仰角为 ,求建筑物 的高度.(参考数据 , , , , ,

如图,小明为了测量校园里旗杆 的高度,将测角仪 竖直放在距旗杆底部 点 的位置,在 处测得旗杆顶端 的仰角为 ,若测角仪的高度是 ,则旗杆 的高度约为 .(精确到 .参考数据: , ,

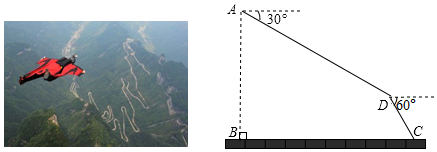
2017年9月8日 日,第六届翼装飞行世界锦标赛在我市天门山风景区隆重举行,来自全球11个国家的16名选手参加了激烈的角逐.如图,某选手从离水平地面1000米高的 点出发 米),沿俯角为 的方向直线飞行1400米到达 点,然后打开降落伞沿俯角为 的方向降落到地面上的 点,求该选手飞行的水平距离 .
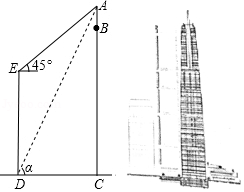
如图,长沙九龙仓国际金融中心主楼 高达 ,是目前湖南省第一高楼,和它处于同一水平面上的第二高楼 高 ,为了测量高楼 上发射塔 的高度,在楼 底端 点测得 的仰角为 , ,在顶端 点测得 的仰角为 ,求发射塔 的高度.
小亮在某桥附近试飞无人机,如图,为了测量无人机飞行的高度 ,小亮通过操控器指令无人机测得桥头 , 的俯角分别为 , ,且 , , 在同一水平线上.已知桥 米,求无人机飞行的高度 .(精确到0.01米.参考数据: ,

如图示一架水平飞行的无人机 的尾端点 测得正前方的桥的左端点 的
俯角为 其中 ,无人机的飞行高度 为 米,桥的长度为1255米.
①求点 到桥左端点 的距离;
②若无人机前端点 测得正前方的桥的右端点 的俯角为 ,求这架无人机的长度 .
